『linear algebra-4』linear mapping
线性映射
本篇是对高等代数中"线性映射"的定义、性质以及定理的速记,不涉及严密的推导证明。
一、映射的概念
映射的定义:设 \(\text{A}\) 和 \(\text{B}\) 是集合,映射 \(f: \text{A} \rightarrow \text{B}\) 表示对于 \(\forall \ a \in \text{A}\),都存在 \(b \in \text{B}\),使得 \(b = f(a)\)
满射 与 单设:设 \(\text{Im}f = f(\text{A}) = \{f(a) \ | a \in \text{A} \}\) 是 \(f\) 的像集
- 满射:若 \(\text{Im}f = \text{B}\),则称 \(f\) 为满射(即 \(\text{B}\) 上每个元素都能取到)
- 单射:若 \(a_1 \ne a_2\),都有 \(f(a_1) \ne f(a_2)\),则称 \(f\) 为单射
若 \(f\) 既是单设,又是满射,则称 \(f\) 是双射(一一对应)
映射的复合运算:设映射 \(f: \text{A} \rightarrow \text{B}\),\(g: \text{B} \rightarrow \text{C}\),则复合映射 \(g \circ f: \text{A} \rightarrow \text{C}\), 即 \(g\circ f(a) = g(f(a))\)
映射具有结合律,即 \(h \circ (g \circ f) = (h \circ g) \circ f\)
逆映射:设 \(f: \text{A} \rightarrow \text{B}\),若存在 \(g: \text{B} \rightarrow \text{A}\),使得 \(g\circ f = f \circ g = \text{I}\),则称 \(g\) 和 \(f\) 互为逆映射,记 \(g = f^{-1}\)
其中 \(\text{I}: \text{A}\rightarrow \text{A}\) 是恒等映射
"逆映射" 与 "一一对应":\(f: \text{A} \rightarrow \text{B}\) 是可逆映射 \(\Leftrightarrow\) \(f\) 是双射
线性映射:设 \(\text{V}\) 和 \(\text{U}\) 是数域 \(\text{K}\) 上的线性空间,映射 \(\phi: \text{V} \rightarrow \text{U}\),\(\alpha, \beta \in \text{V}\),\(k \in \text{K}\),若同时满足
- \(\phi(\alpha + \beta) = \phi(\alpha) + \phi(\beta)\)(在两个空间上保持加法)
- \(\phi(k\cdot \alpha) = k\cdot \phi(\alpha)\)(在两个空间上保持数乘)
则称 \(\phi\) 是线性映射;若 \(\text{V} = \text{U}\) 则称 \(\phi\) 是线性变换;若 \(\phi\) 是双射则称 \(\phi\) 是线性同构,记作 \(\text{V} \cong \text{U}\)
线性同构是等价关系:满足三条性质
- 自反性:在线性同构 \(\text{I}: \text{V} \rightarrow \text{V}\) 下,\(\text{V} \cong \text{V}\)
- 对称性:设 \(\phi: \text{V} \rightarrow \text{U}\) 是线性同构,\(\text{V} \cong \text{U}\),则有 \(\phi^{-1}: \text{U} \rightarrow \text{V}\) 也是线性同构,即 \(\text{U}\cong \text{V}\)
- 传递性:设 \(\phi: \text{V} \rightarrow \text{U}\),\(\psi: \text{U} \rightarrow \text{W}\) 都是线性同构,则有 \(\psi \circ \phi: \text{U} \rightarrow \text{W}\) 也是线性同构
两个线性空间之间存在线性同构 \(\Leftrightarrow\) 两个线性空间的维数相同
线性映射的集合:设 \(\text{V}\) 和 \(\text{U}\) 是线性空间,记 \(\mathcal{L}(\text{V}, \text{U})\) 是 \(\text{V} \rightarrow \text{U}\) 间线性映射的集合,\(\phi, \psi \in \mathcal{L}(\text{V}, \text{U})\)
- 映射加法:\((\phi + \psi)(\alpha) = \phi(\alpha) + \psi(\alpha)\)
- 映射数乘:\((k\cdot \phi)(\alpha) = k \cdot \phi(\alpha)\)
则 \(\mathcal{L}(\text{U}, \text{V})\) 在这样定义的加法和数乘条件下构成一个 \(\text{K}\) 上的 线性空间;\(\mathcal{L}(\text{U})\) 是线性变换构成的线性空间
线性变换的复合:设 \(\phi \in \mathcal{L}\),定义 \(\phi^n = \phi \circ \dots \circ \phi\),与方阵定义十分类似!
\(\phi^n \circ \phi^m = \phi^{n+m}\),\((\phi^n)^m = \phi^{nm}\)
若 \(\phi\) 是自同构,则 \(\phi^{-n} = (\phi^{-1})^n = (\phi^n)^{-1}\),\((k \cdot \phi)^{-1} = k^{-1}\phi^{-1}\)
若 \(\phi, \psi\) 都是自同构,则 \(\phi \psi\) 也是自同构,且 \((\phi\psi)^{-1} = \psi^{-1}\phi^{-1}\)
注意:一般而言,\(\phi \psi \ne \psi \phi\),故 \((\psi\phi)^n \ne \psi^n \phi^n\)
二、线性映射的矩阵
线性扩张定理:设 \(\text{V}\) 和 \(\text{U}\) 是两个线性空间,\(\{e_1, \dots, e_n\}\) 是 \(\text{U}\) 的基,\(\{\beta_1, \dots, \beta_n\}\) 是 \(\text{V}\) 中的一组向量
则必存在唯一的线性映射 \(\phi: \text{V} \rightarrow \text{U}\),使得 \(\phi(\alpha_i) = \beta_i\)(\(1 \le i \le n\))给定基下的表示矩阵:设 \(\phi: \text{V}^n \rightarrow \text{U}^m\) 是线性映射,\(\{e_i\}_{1\dots n}\) 是 \(\text{V}\) 的基,\(\{f_i\}_{1\dots m}\) 是 \(\text{U}\) 的基,将 \(\text{V}\) 中的基映射到 \(\text{U}\) \[ \begin{cases} \phi(e_1) = a_{11}f_1 + \dots + a_{m1}f_m \\ \qquad \vdots \\ \phi(e_n) = a_{1n}f_1 + \dots + a_{mn}f_m \\ \end{cases} \] 则 \(f_i\) 前的矩阵的转置 \(\text{A}_{m\times n}\) 记作给定基 \(\{e_i\}_{1\dots n}\) 下的表示矩阵,可写成 \((\phi(e_1), \dots, \phi(e_n)) = (f_1, \dots, f_m)\text{A}\)
任取 \(\alpha = \sum_{i=1}^n \lambda_i e_i\),记映射的像 \(\phi(\alpha) = \sum_{i=1}^m \mu_i f_i\),结合上式
可得到坐标向量和表示矩阵的关系,即: \[ \begin{bmatrix} \mu_1 \\ \vdots \\ \mu_m \end{bmatrix} = \text{A} \begin{bmatrix} \lambda_1 \\ \vdots \\ \lambda_n \end{bmatrix} \] 即新坐标向量 等于 表示矩阵乘以旧坐标向量
"线性映射" 与 "矩阵":
映射 \(\text{T}: \mathcal{L}(\text{U}^n, \text{V}^m) \rightarrow \text{M}_{m\times n}(\text{K})\) 是线性同构;任取 \(\phi \in \mathcal{L}\),有表示矩阵 \(\text{A} = \text{T}(\phi)\)
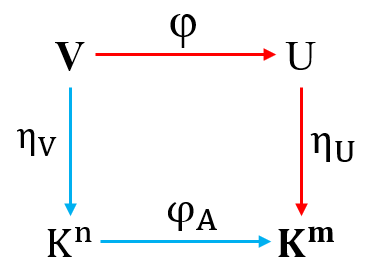
交换图:沿两个对象的任意路径的态射,所得结果均相等
符号定义:
- \(\eta_{\text{V}}: \text{V}^n \rightarrow \text{K}^n\) 是 \(\text{V}\) 上抽象向量到坐标向量的线性同构(给定基 \(\{e_i\}_{1\dots n}\))
- \(\eta_{\text{U}}: \text{U}^m \rightarrow \text{K}^m\) 是 \(\text{U}\) 上抽象向量到坐标向量的线性同构(给定基 \(\{f_i\}_{1\dots m}\))
- \(\phi_\text{A}: \text{K}^n \rightarrow \text{K}^m\) 是 两个空间上坐标向量间的线性同构,即 \(\eta = \text{A}_{m\times n}\lambda\)(由表示矩阵给出)
任取 \(\phi, \psi \in \mathcal{L}\),存在以下交换图,满足 \(\eta_\text{U} \circ \phi = \phi \circ \eta_{\text{V}}\)(左上 \(\Rightarrow\) 右下,两条路径)
"复合映射" 与 "矩阵相乘":设 \(\phi: \text{V}^n \rightarrow \text{U}^m\),\(\psi: \text{U}^m \rightarrow \text{W}^p\) 为线性映射
对于复合映射 \(\psi \phi: \text{V}^n \rightarrow \text{W}^p\),有矩阵乘法关系 \(\text{T}(\psi\phi)_{p\times n} = \text{T}(\psi)_{p\times m} \cdot \text{T}(\phi)_{m\times n}\)
"映射性质" 与 "矩阵性质":设 \(\text{T}: \mathcal{L}(\text{V}) \rightarrow \text{M}_n(\text{K})\)
\(\text{T}(\text{I}_\text{V}) = \text{I}_n\),即恒等变换对应单位矩阵
\(\phi \in \mathcal{L}(\text{V})\),则 \(\phi\) 是自同构(可逆) \(\Leftrightarrow\) \(\text{T}(\phi)\) 可逆(在任意基下都非奇异)
两组表示矩阵的关系:设 \(\phi \in \mathcal{L}(\text{V})\),\(\text{V}^n\) 的两组基为 \(\{e_i\}_{1\dots n}\) 和 \(\{f_i\}_{1\dots n}\),从基 \(e_i\) 到 基 \(f_i\) 的过渡矩阵为 \(\text{P}\)
设 \(\phi\) 在基 \(e_i\) 下的表示矩阵为 \(\text{A}\),即 \((\phi(e_1), \dots, \phi(e_n)) = (e_1, \dots, e_n)\text{A}\);同理设 \(\phi\) 在基 \(f_i\) 下的表示矩阵为 \(\text{B}\)
则有 \(\text{B} = \text{P}^{-1}\text{AP}\),即同一线性变换在不同基下的表示矩阵是相似的,记作 \(\text{A} \approx \text{B}\)
相似关系是等价关系:满足三条性质
- 自反性:\(\text{A} = \text{I}^{-1}\text{A}\text{I}\),即 \(\text{A} \approx \text{A}\)
- 对称性:设 \(\text{A} \approx \text{B}\),则有 \(\text{B} \approx \text{A}\)
- 传递性:设 \(\text{A} \approx \text{B}\),且 \(\text{B} \approx \text{C}\),则有 \(\text{A} \approx \text{C}\)
三、像与核
像空间 与 核空间:设线性变换为 \(\phi: \text{V}^n \rightarrow \text{U}^m\)
- 像 \(\text{Im}(\phi) = \{\phi(v) \ | v \in \text{V} \ \}\),且 $() $
- 核 \(\text{ker}(\phi) = \{v \in \text{V} \ | \phi(v) = \textbf{0}_{\text{U}} \ \} \subseteq \text{V}\)
且 \(\text{Im}(\phi)\) 是 \(\text{U}\) 的子空间,\(\text{Ker}(\phi)\) 是 \(\text{V}\) 的子空间
"映射性质" 与 "像与核":
- \(\phi\) 是单射 \(\Leftrightarrow\) \(\text{ker}(\phi) = 0\)
- \(\phi\) 是满射 \(\Leftrightarrow\) \(\dim (\text{Im}(\phi)) = \dim \text{U}\),即只需要考虑维数就能判断是否可逆
像空间与核空间的维数:
- \(\text{r}(\phi) = \dim (\text{Im} (\phi))\),即把像空间的维数看作 \(\phi\) 的秩
- \(\dim (\text{ker}(\phi))\) 记为 \(\phi\) 的零度
\(\text{r}(\phi)\) \(+\) \(\dim (\text{ker}(\phi))\) \(= n\):设 \(\text{V}\) 基为 \(\{e_i\}_{1\dots n}\),\(\text{U}\) 基为 \(\{f_i\}_{1\dots m}\),设 \(\phi\) 在给定的两组基下的表示阵为 \(\text{A}_{m\times n}\)
则有 \(\text{r}(\phi) = \text{r(A)}\),且 \(\dim (\text{ker}(\phi)) = n - \text{r(A)}\)(线性空间的维数公式)
"映射性质" 与 "表示矩阵":设 \(\phi: \text{V}^n \rightarrow \text{U}^m\) 在两组基下的表示矩阵为 \(\text{A}_{m\times n}\)
- \(\phi\) 是单射 \(\Leftrightarrow\) \(\text{A}\) 行满秩,即 \(\text{r(A)} = m\)
- \(\phi\) 是满射 \(\Leftrightarrow\) \(\text{A}\) 列满秩,即 \(\text{r(A)} = n\)
同维数线性映射:设 \(\phi: \text{U}^n \rightarrow \text{V}^n\),则有 \(\phi\) 是双射 \(\Leftrightarrow\) \(\phi\) 是单射 \(\Leftrightarrow\) \(\phi\) 是满射