『computer organization-1』digital circuit
数字电路
一、逻辑代数
逻辑运算优先级降序:括号 > 非 > 与(乘) > 异或 > 或(加)
逻辑代数基本定律:设 A \(\in \{0, 1\}\) 是逻辑变量
- 自等律:A + 0 = A,A \(\cdot\) 1 = A
- 0-1 律:A + 1 = 1,A \(\cdot\) 0 = 0
- 交换律:A + B = B + A,A \(\cdot\) B = B \(\cdot\) A
- 结合律:(A + B) + C = A + (B + C),(A \(\cdot\) B) \(\cdot\) C = A \(\cdot\) (B \(\cdot\) C)
- 分配律:A(B + C) = AB + AC(对加法分配),A + BC = (A + B)(A + C)(对乘法分配)
代入定理:在一个逻辑等式中,用另一个函数式代入该等式中某个同名变量的所有位置,等式仍然成立
注意:代入定理扩大了基本逻辑公式的使用范围
反演定理⭐:设原逻辑函数为\(\text{F}\),对F中的所有元素按以下方式替换
- 将乘法换成加法,将加法换成乘法
- 将 0 换成 1,将 1 换成 0
- 将原变量换成反变量,将反变量换成原变量
所得到的新函数 \(\overline{\text{F}}\) 即为反演式;反演式可用于化简,比如先对 \(\text{F}\) 取反演得到 \(\overline{\text{F}}\),再化简 \(\text{F} = \overline{\overline{\text{F}}}\)
注意:对于第三条替换原则,不属于单个变量的非运算在变换中不变,如 \(\overline{\text{A+B}}\) 仍是 \(\overline{\text{A+B}}\)
对偶定理⭐:设原逻辑函数为F,对F中的所有元素按如下方式替换
- 将乘法换成加法,将加法换成乘法
- 将 0 换成 1,将 1 换成 0
所得到的新函数 F' 与 F 互为对偶式,且对偶公式一定成立(见分配律的两种情况)
标准表达式:包括"最大"和"最小"表达式
- 最小项表达式:全部由最小项构成的积之和式
- 最大项表达式:全部由最大项构成的和之积式
最小推导法:将输出为 1 对应的输入组合写成乘积项的形式,对于乘积项的变量
- 若其取值为 1,在乘积项中用原变量表示
- 若其取值为 0,在乘积项中用反变量表示
再将所有输出为 1 的组合对应的乘积项相加得到最终的逻辑函数 \(\text{F}\)
最大项:各变量(或其反变量)的求和,如 \(\text{A + B +}\overline{\text{C}}\)
最大项的顺序:最大项中原变量用 0 表示,反变量用 1 表示,用最大项二进制数表示顺序
如 \(\overline{\text{A}} + \overline{\text{B}} + \overline{\text{C}}\) 表示为 111(最大的最大项),\(\text{A} + \overline{\text{B}} + \overline{\text{C}}\) 表示为 011
最大项的相邻性:若 2 个最大项只有 1 个变量分别以原变量和反变量的形式出现,记这两个最大项相邻
最大项的性质:
- 对于任意最大项,仅有一组变量取值使其为 0(所有变量同时取 1),其余情况都是 1
- 全体最大项之积为 0(\(\text{A}\overline{\text{A}} = 0\)),任意两个最大项之和为 1(\(\text{A} + \overline{\text{A}} = 1\))
- 相邻两个最大项之积可以合并为一个和项,如 \((\overline{\text{A}} + \text{B})(\text{A} + \text{B}) = \text{B}\)(消去变化的量)
最大项推导法:将输出为 0 对应的输入组合写成和项形式,对于和项的变量:
- 若其取值为 0,在和项中用原变量表示
- 若其取值为 1,在和项中用反变量表示
再将所有输出为 0 的组合对应的和项相乘得到最终的逻辑函数 \(\text{F}\)
注意:"最大项"推导 和 "最小项"推导是相反的,比如选取输出为1 or 0的输入组合,原变量/反变量对应为1 or 0
二、组合逻辑设计
组合逻辑特点:无记忆的电路,输出信号随输入信号的消失而消失
- 由逻辑门(与或非)电路组成
- 输出不能直接反馈到输入(无环路),且不具备记忆存储电路
- 当前的输出仅由当前的输入决定,响应速度较快
半加器:对两个 1bit 二进制数相加,向高位进位的同时不考虑来自低位的进位
- 输入两个 1bit 二进制数 \(\text{A, B}\),输出两个 1bit 二进制数 求和 \(\text{SO}\) 与 进位 \(\text{CO}\)
- 真值映射:\(\text{SO} = \text{A} \oplus \text{B}\)(异或、无低位进位),\(\text{CO} = \text{AB}\)(向高位进位,同"1"进位)
全加器:对三个 1bit 二进制数,向高位进位的同时考虑来自低位的进位
- 输入三个 1bit 二进制数 \(\text{A, B}\) 以及低位进位 \(\text{CI}\),输出两个 1bit 二进制数 求和 \(\text{SO}\) 和 进位 \(\text{CO}\)
- 真值映射:\(\text{SO} = \text{A} \oplus \text{B} \oplus \text{CI}\),\(\text{CO} = \text{A }\overline{\text{B}}\text{ CI} + \overline{\text{A}} \text{ B} \text{ CI} + \text{AB}\)
多位加法器:能实现多位二进制数相加的电路(上面两个都是 1bit 二进制)
串行进位加法器:低位全加器的 \(\text{CO}\) 接 高位全加器 的 \(\text{CI}\),电路简单,但由于是串行所以时延长
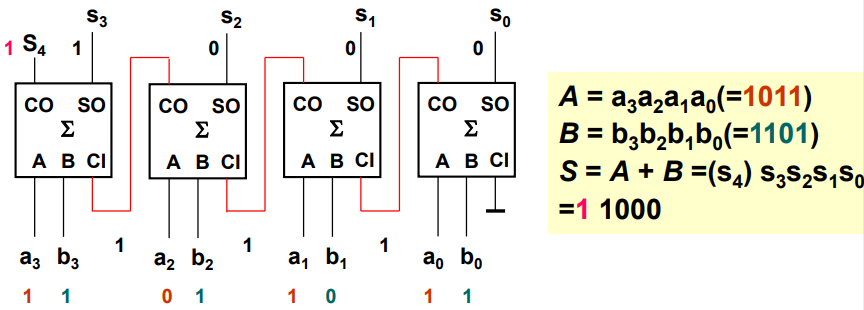
并行进位加法器:设置专用的进位形成电路提前把各进位算出来,又称超前进位加法器,时延短但电路复杂
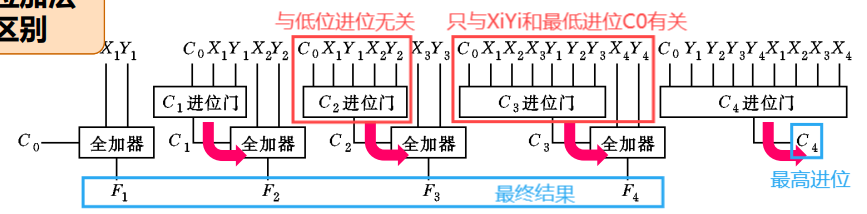
分组并行进位加法器:组内并行,组间传递
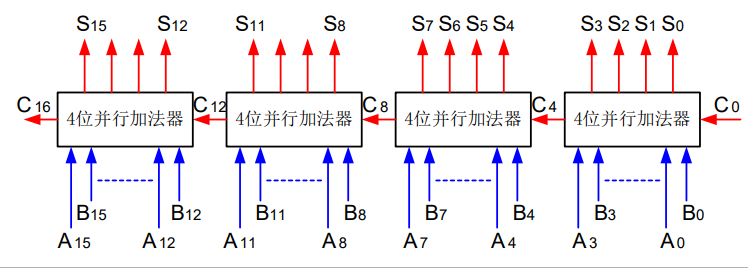
减法运算电路:数字在计算机中是以补码形式存储的
补码运算:\([\text{A} + \text{B}]_{\text{补}} = [\text{A}]_{\text{补}} + [\text{B}]_{\text{补}}\),同理 \([\text{A} - \text{B}]_{\text{补}} = [\text{A}]_{补} + [-\text{B}]_{补}\)
整数的补码表示:设 \([x]_{补} = x_{n-1}\dots x_{0}\),则 \([-x]_{补} = \overline{x_{n-1}} \dots \overline{x_{0}} + 1\),即按位取反再加一
故减法电路和加法电路是可以共用的,即 \([\text{A} - \text{B}]_{\text{补}} = [\text{A}]_{补} + \overline{[\text{B}]_{补}} + 1\)
运算溢出:分为加法溢出和减法溢出
- 加法溢出:符号位相同的两数相加,结果的符号位与加数符号位相反
- 减法溢出:符号位相异的两数相减,结果的符号位与减数符号位相同
双符号位:"00" 表示正、"11" 表示负,结果符号位出现 "01" 或 "10" 表示溢出
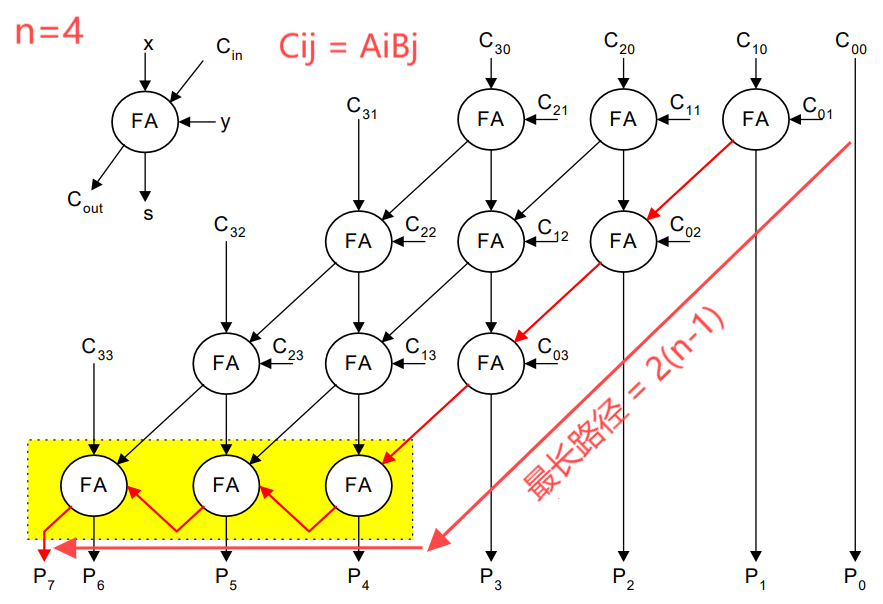
乘法器:\(n\) 位的阵列乘法,需要 \(n(n-1)\) 个全加器 FA
比较器:比较两个二进制数的大小
- 一位比较器:讨论 \(\text{F}_{\text{A} > \text{B}}\),\(\text{F}_{\text{A} = \text{B}}\),\(\text{F}_{\text{A} < \text{B}}\) 输出为 1 对应的输入组合(x4),分别列出最小项表达式即可
- 多位比较器:由多个 1bit 比较器组成,优先比较高位 bit,直至比出大小
编码器 与 解码器:
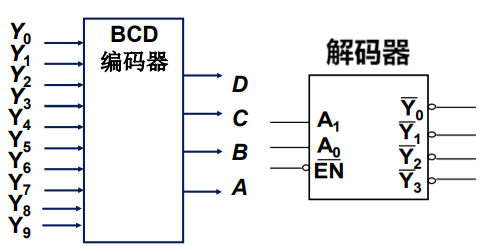
- 编码器:将独热信号转换为一组二进制编码输出
- BCD 编码器(10 bit \(\rightarrow\) 4 bit):将 十进制独热信号 0~9 转换为 对应二进制编码(进制转换)
- \(2^n \sim n\) 编码器:将 \(2^n\) 个独热信号 转换为 对应的 \(n\) 位二进制编码(如38编码器)
- 解码器:执行编码器的逆运算
- BCD 解码器(4 bit \(\rightarrow\) 10 bit):将 二进制编码 转换为 对应的十进制独热信号(进制转换)
- \(n \sim 2^n\) 解码器:将 \(n\) 位二进制编码 转换为 对应的 \(2^n\) 个独热信号
- 7 段数码管显示解码器:将 二进制值 转换为 7段数码管 的开闭
注意:由"独热"可知,编码器任何时刻最多允许一个输入有效,解码器任何时刻最多允许一个输出有效
- 编码器:将独热信号转换为一组二进制编码输出
多路复用器:从一组输入(\(\{\text{D}_i\}_{0\dots n-1}\))中选出(控制为 \(\{\text{A}_i\}_{0\dots (\log n)-1}\))一个作为输出,又称 \(n\)选1 Mux
数据选择器:当 \(\text{A}\) 作为控制端时,可从 \(n\) 个输入中选择一个作为输出(原始用途)
设计任意组合逻辑:当 \(\text{D}\) 为控制端时,可通过对 \(\text{D}\) 赋予固定的一组值,实现任意组合逻辑
- 写出组合逻辑函数:将函数 \(\text{F}\) 化为最小项之和的标准形式,如 \(\text{F} = m_1 + m_3\)
- 写出多路复用器输出:\(\text{Y} = m_0\text{D}_0 + m_1\text{D}_1 + m_2\text{D}_2 + m_3\text{D}_3\)
- 对照上两式,令 \(\text{F} = \text{Y}\),写出固定的 \(\text{D}_0 = 0\),\(\text{D}_1 = 1\),\(\text{D}_2 = 0\),\(\text{D}_3 = 1\)
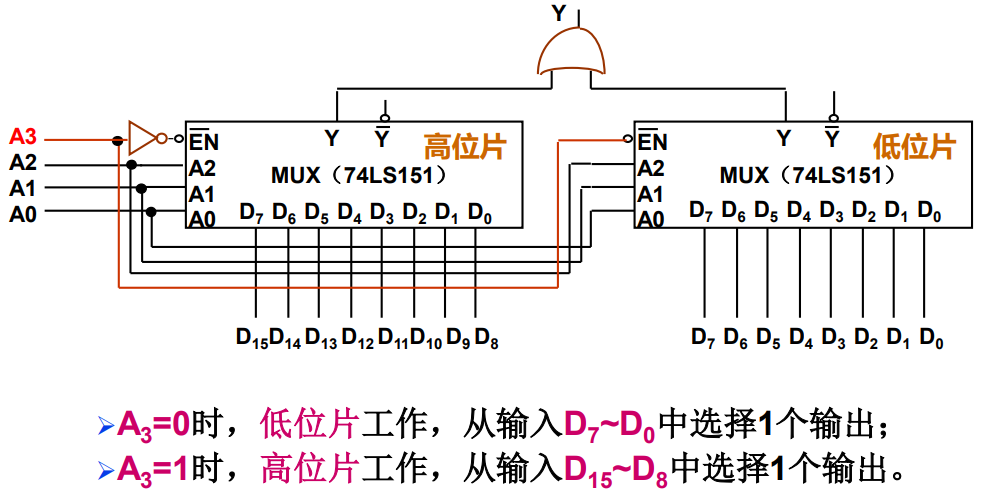
扩展多路复用器:新增 \(\text{A}_{\log n}\) 接低片的使能端,\(\overline{\text{A}_{\log n}}\) 接高片的使能端,从而扩展输入 \(\text{D}\) 的范围
竞争 与 冒险:
竞争:某一个输入变量通过多条延迟不同的路径传输到输出端,到达时间有先有后
冒险:因输入端竞争导致的输出端产生不正常的干扰冒充信号(尖锋毛刺)
判断冒险方法:
代数法:在某些输入条件下,\(\text{F}\) 可化简为 \(\text{A} + \overline{\text{A}}\) 或 \(\text{A}\overline{\text{A}}\) 的形式
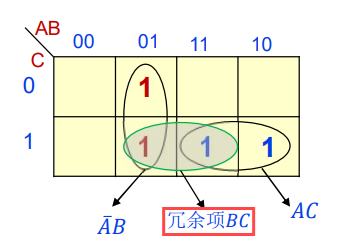
卡诺图法:\(\text{F}\) 的最小项表达式的乘积项间存在 相切
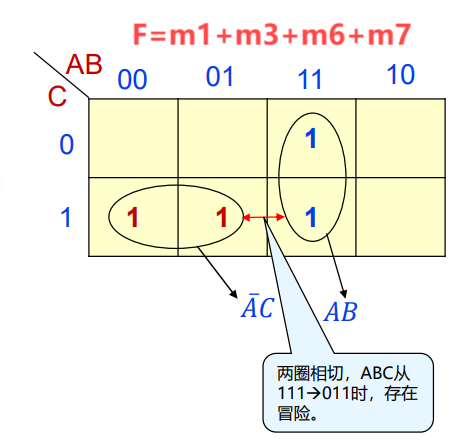
解决冒险方法:尝试消除互补变量(改),或在 \(\text{F}\) 中添加新的冗余项覆盖相切位置(增)
以后者为例,设 \(\text{F} = \text{AC} + \overline{\text{A}}\text{B}\),当 \(\text{B} = \text{C} = 1\) 时 \(\text{F} = \text{A} + \overline{\text{A}}\) 存在冒险;故增加 \(\text{BC}\),防止出现毛刺(\(\text{BC}=1\))
三、时序逻辑设计
时序电路的特点:当时的输出与当时的输入和原来的状态决定,具有 "记忆功能"
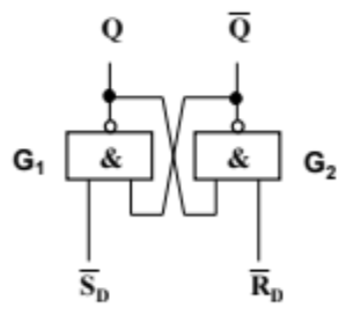
基本RS锁存器:具有"置0"、"置1"、"保持"功能,输入两个变量 \(\text{S}_\text{D}, \text{R}_\text{D}\),输出两个互非状态 \(\text{Q}\) 和 \(\overline{\text{Q}}\)
- 特性方程:\(\text{Q}_{n+1} = \text{S}_\text{D} + \overline{\text{R}_\text{D}} \text{Q}^n\),同时满足约束 \(\text{S}_\text{D} \text{R}_\text{D} = 0\)(两个输入不许同时激活)
- 功能描述:\(\text{S}_\text{D} = \text{R}_\text{D} = 0\) 保持,\(\text{S}_\text{D} = 1, \ \text{R}_\text{D} = 0\) 置1,\(\text{S}_\text{D} = 0, \ \text{R}_\text{D} = 1\) 置0
注意:下标 \(\text{D}\) 指 Direct,表示输入信号直接控制锁存器输出
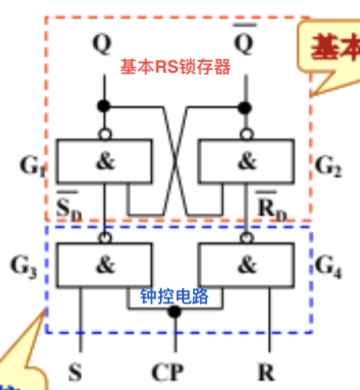
钟控RS锁存器:在基本锁存器的基础上新增时钟控制信号 \(\text{CP}\) 控制输入 \(\text{R}\) 和 \(\text{S}\)
钟控电路:\(\text{S}_\text{D} = \text{S} \cdot \text{CP}\),\(\text{R}_\text{D} = \text{R} \cdot \text{CP}\)
锁存器电路:与基本RS锁存电路相同,其输入是钟控电路的输出 \(\text{S}_\text{D}, \text{R}_\text{D}\)
功能描述:当 \(\text{CP} = 0\) 时,\(\text{S}_\text{D} = \text{R}_\text{D} = 0\) 始终保持;当 \(\text{CP} = 1\) 时,整个电路功能与基本锁存器相同
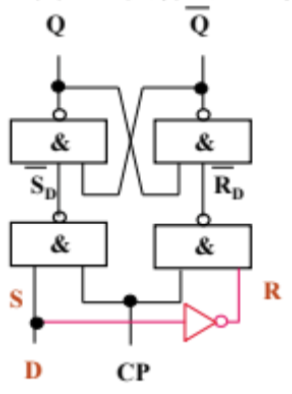
钟控D锁存器:消除RS锁存器的不确定状态(\(\text{S}_\text{D} = \text{R}_\text{D} = 1\)),将输入从两个改成一个 \(\text{D}\)
- 钟控电路:\(\text{S}_\text{D} = \text{D} \cdot \text{CP}\),\(\text{R}_\text{D} = \overline{\text{D}} \cdot \text{CP}\)(相当于 \(\text{S}\) 和 \(\text{R}\) 总是互非的)
- 特性方程:\(\text{Q}^{n+1} = \text{D}\)(当 \(\text{CP} = 1\) 时),当 \(\text{CP} = 0\) 时保持原态(时钟就是使能端)
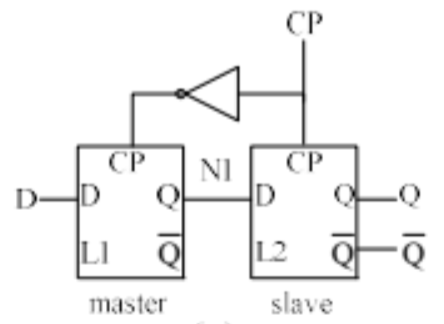
D触发器:由两个D锁存器组成(主锁存器 + 从锁存器)
- 功能描述:当 \(\text{CP} = 0\) 时,\(\text{Q}_{\text{master}} = \text{D}\),但 \(\text{Q}_\text{slave}\) 仍被抑制保持;当 \(\text{CP}\) 跳升到 \(1\) 时,\(\text{Q}_\text{slave} = \text{D}\),\(\text{Q}_\text{master}\) 不变
- 使能端:用 Mux 选择 \(\text{Q}\) 与 \(\text{D}\),当 \(\text{EN} = 0\) 时,触发器保持原态;否则触发器随时钟跳变将 \(\text{Q}\) 更新为 \(\text{D}\)
- 复位端:用 And 输入 \(\text{D}\) 与 \(\overline{\text{RESET}}\),当 \(\text{RESET} = 0\) 时,触发器正常工作;否则触发器始终更新为 \(0\)(复位)
JK触发器:在钟控RS锁存器基础上增加两条反馈线,并将 S/R 改成 J/K,功能更强大且无输入约束
- 功能描述:当 \(\text{CP} = 1\) 时,支持 "保持"(0/0)、"置0"(0/1)、"置1"(1/0)、"翻转"(1/1),扩展了翻转功能 \(\text{Q}^{n+1} = \overline{\text{Q}^n}\)
- 特性方程:\(\text{Q}^{n+1} = \text{J}\overline{\text{Q}^n} + \text{K}\overline{\text{Q}^n}\)(当 \(\text{CP} = 1\) 时),当 \(\text{CP} = 0\) 时保持原态(时钟就是使能端)
四、有限状态机
FSM 模型:表示有限个状态以及这些状态之间的转移和动作等行为等离散数学模型
有限状态机等种类:主要在 "输出" 上有差异
- Moore 型状态机:输出仅与当前状态有关,与当前输入无关
- Mealy 型状态机:输出与当前状态和当前输入有关
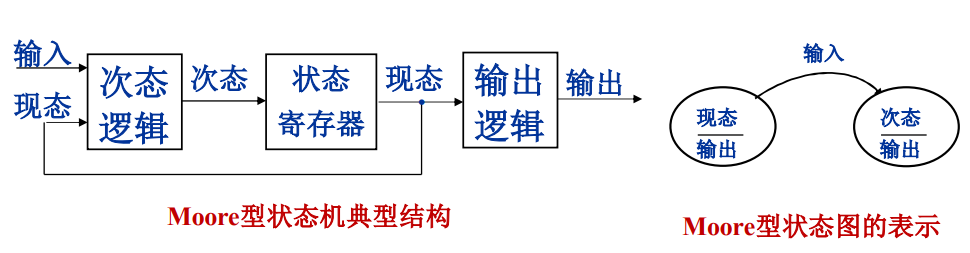
Moore 型状态机:
- 组成:次态逻辑(当前状态 + 当前输入 \(\Rightarrow\) 下一状态),状态寄存器,输出逻辑(当前状态 \(\Rightarrow\) 当前输出)
- 表示方法:状态图 or 状态表(当前状态|下一状态|输出)
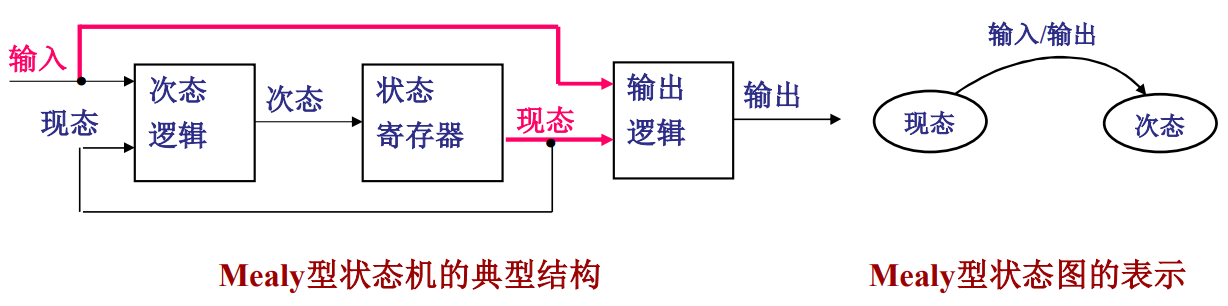
Mealy 型状态机:
- 组成:次态逻辑(当前状态 + 当前输入 \(\Rightarrow\) 下一状态),状态寄存器,输出逻辑(当前状态 + 输入 \(\Rightarrow\) 当前输出)
- 表示方法:状态图 or 状态表(当前状态 | 输入 | 下一状态 | 输出)