『paper-NLP-1』《Attention is all you need》
《Attention is all you need》
From Advances in Neural Information Processing Systems (2017)
一、架构总览
模型结构:由左边的 encoder 和 右边的 decoder 组成,架构总览图如下:
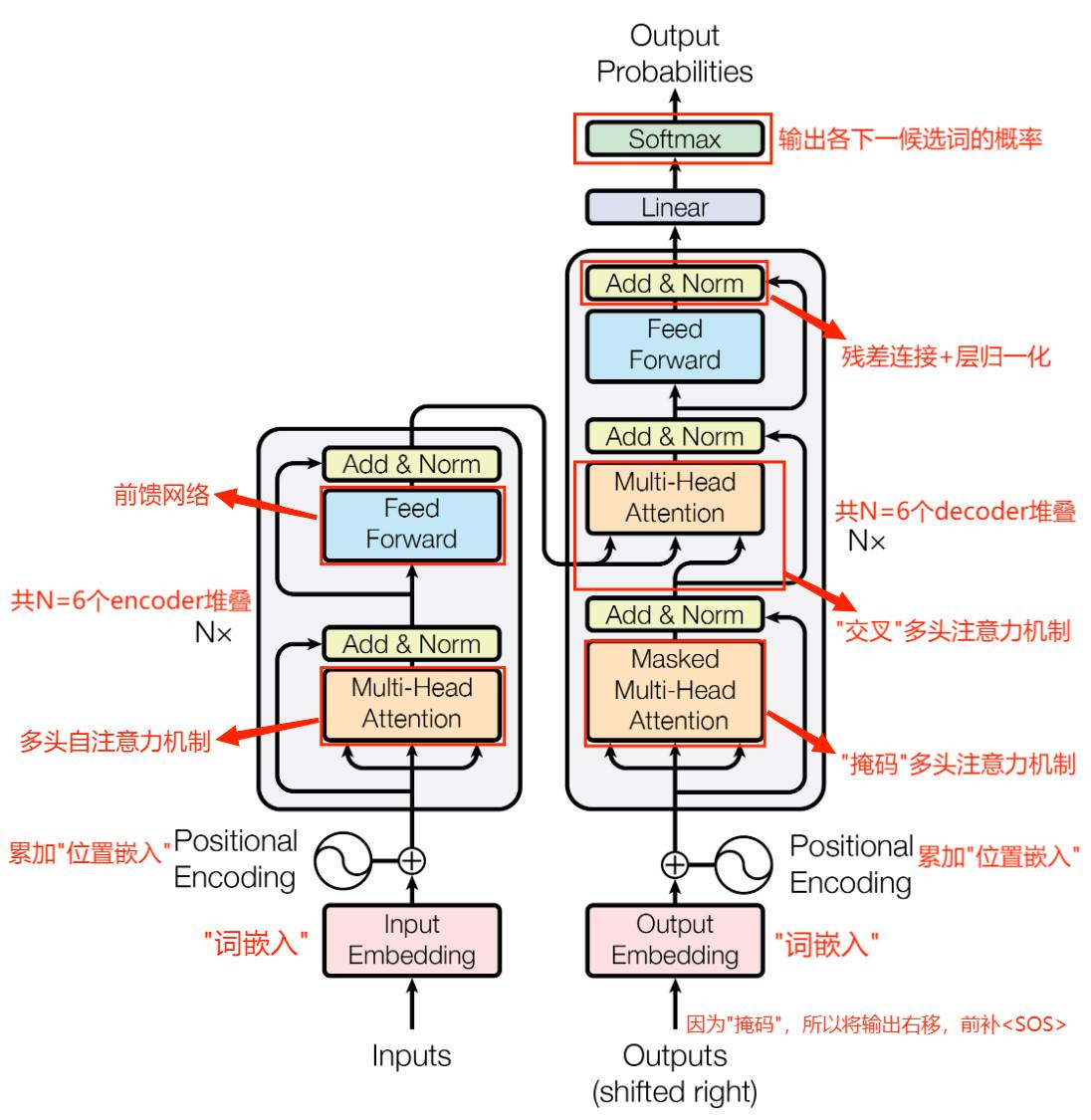
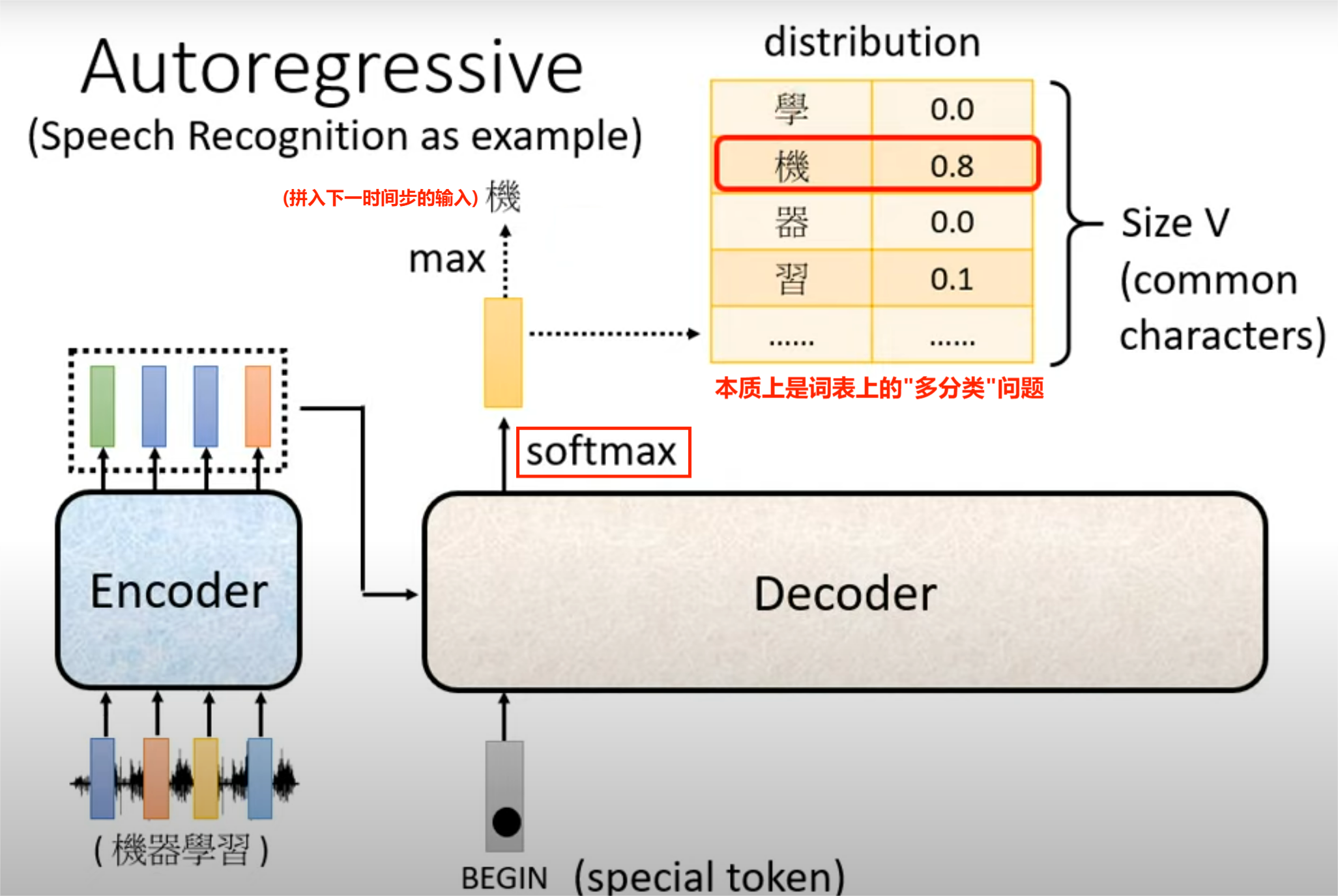
推理流程:这里以"机器翻译"为例子,输入中文"我爱你"、输出英文"i love you <EOS>"
encoder 词嵌入:中文输入左侧的"encoder"模块,将中文单词"我"、"爱"、"你"分别转换成对应的词向量
encoder 位置嵌入:将三个中文单词对应的词向量分别进行位置编码,再执行 词向量 + 位置向量 操作
注意:每个单词的词向量和位置向量是等长度的,保证两个向量可以逐元相加
encoder 注意力:根据输入的每个词向量(经过位置编码)计算 Q、K、V 矩阵
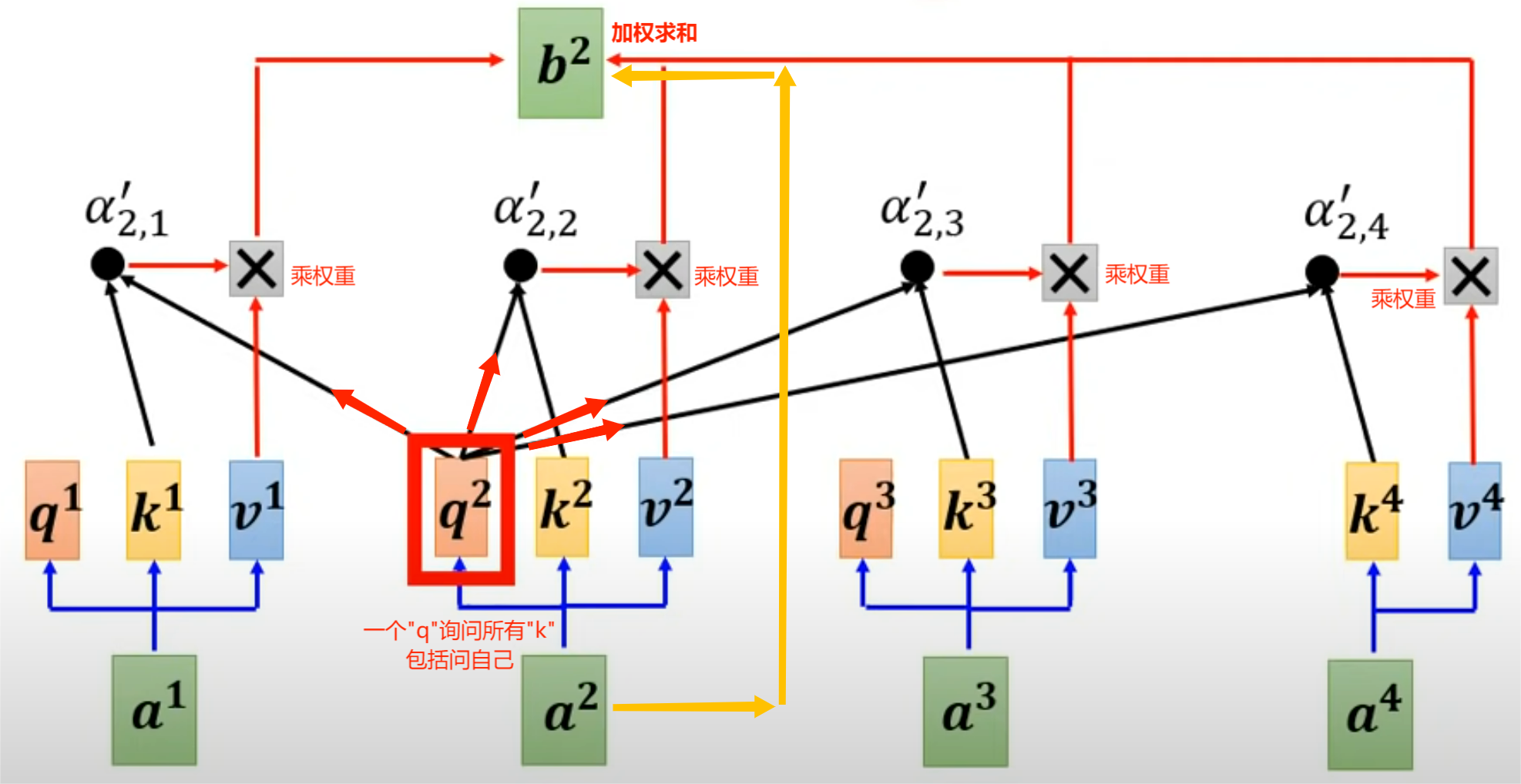
利用 Q、V 矩阵计算两两词向量之间的 注意力分数\(\alpha_{ij}\),获得序列内部相关性信息
将 注意力分数 结合 V 矩阵进行加权求和计算每个词向量的重构词向量
encoder 输出:将重构词向量输入前馈网络(两个全连接层),产生编码器输出
decoder 词嵌入:由于使用了"掩码"机制,所以将整个序列向后平移一位,开头插入"<SOS>",并将其转成词向量输入
decoder 位置嵌入:同 encoder 位置嵌入
decoder 掩码注意力:类似 encoder,生成下一个单词对应的query,作为交叉注意力机制的输入矩阵Q
注意:decoder掩码机制是"auto-regressive"的,如果当前已经输出了"i love"、下一个时间步将以"<SOS> i love"为已知信息(而无法看到后续的单词)输出下一个单词"you"
decoder 交叉注意力:以 encoder 的输出作为矩阵 K、V,以 decoder 的当前输入作为 Q,生成下一个单词的重构词向量
decoder 输出:同 encoder 输出
transformer 输出:经过全连接 + softmax 层,输出当前时间步下词表中每个单词的概率,输出预测的单词(应当是"i")
下一时间步以"<SOS>"和"i"为已知信息,尝试预测下一个单词"love";不断重复直至预测出"<EOS>"
训练流程:encoder 部分与推理阶段基本无差异,但 decoder 部分采用的是 "teaching-forcing" 方案
decoder 每生成一个新的单词,计算其与Ground-Truth单词之间的交叉熵损失(看作是"多分类"问题)
decoder 不像推理阶段将当前输出的单词拼接回下一时间步的输入,而是输入下一预期的正确单词
保证训练阶段 decoder 生成的单词不会出现"一步错步步错"的问题
二、词嵌入
- 单词的表示:一个单词 \(\Rightarrow\) 一个数值表示的词嵌入向量
- 词嵌入向量:单词在词表中的序号 \(\Rightarrow\) 嵌入词典中某行向量的索引,从而建立单词到数值向量的映射
- 常见的词嵌入方法:包括 Word2Vec、GloVe 等预训练嵌入模型
三、位置嵌入
位置的表示:一个单词 \(\Rightarrow\) 一个数值表示的位置编码向量
注意:由于 Transformer 本身无法捕捉序列内部单词间的顺序关系,所以需要对单词的位置进行编码
位置嵌入向量:单词在句子中的位置 \(\Rightarrow\) 一个位置编码向量;设单词在句子中的位置是 \(pos\),\(d\) 表示位置嵌入维度(= 词嵌入维度) \[ \text{位置嵌入矩阵 PE} = \begin{cases} \text{PE}_{(pos, 2i)} = \sin(\dfrac{pos}{10000^{2i / d}}) \\ \text{PE}_{(pos, 2i+1)} = \cos(\dfrac{pos}{10000^{2i / d}}) \end{cases} \] 上式分别定义了奇数维度(\(2i + 1\))的 \(\text{PE}\) 和偶数维度(\(2i\))的位置矩阵 \(\text{PE}\);该编码方式有以下优点:
- 每个位置都有唯一的编码,且编码是有界的([-1, 1])
- 由三角函数的和角公式可知,\(\text{PE}_{(pos+\textbf{k}, i)}\) 可由 \(\text{PE}_{pos, i}\) 线性表示,故该编码方式可以表示任意比训练集句长更大的位置
- 位置编码的点积结果(\(\text{PE}_{(pos, 2i)} \text{PE}_{(pos, 2i+1)}\))仅与相对位置差有关,故可以建模相对位置关系
将 词嵌入向量 和 位置嵌入向量 逐元素相加,就得到了 encoder 和 decoder 的输入
四、自注意力机制⭐
什么是"注意力机制":建立同一句子中不同位置单词之间的内部联系(\(\text{QK}^T\)),再用 \(\text{V}\) 重建原句单词
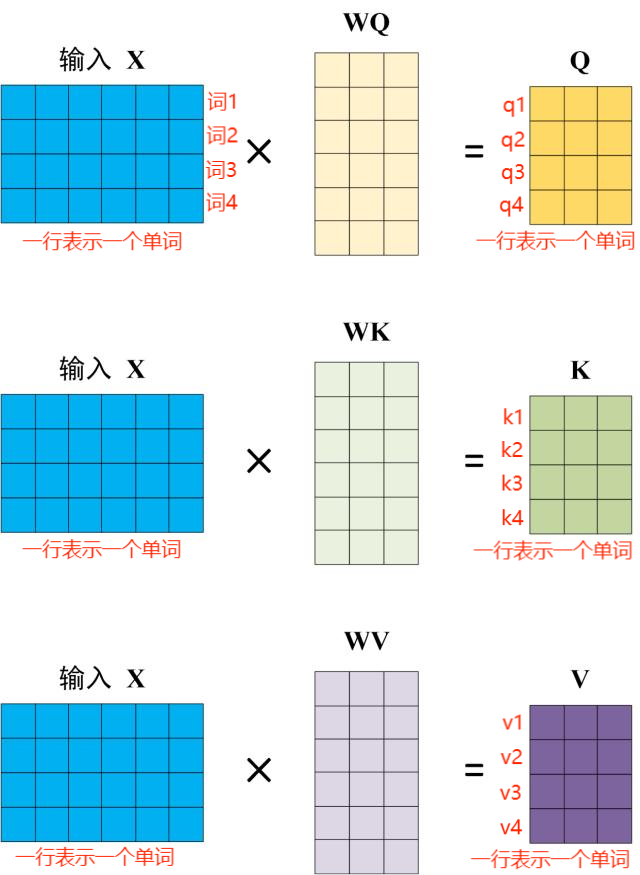
\(\text{Q}\)、\(\text{K}\)、\(\text{V}\) 矩阵的计算:让词嵌入矩阵 \(\text{X}\) 分别乘以矩阵 \(\text{W}_\text{Q}\)、\(\text{W}_{\text{K}}\)、\(\text{W}_{\text{V}}\),得到每个词向量对应的 latent representation
注意:本例以及下面的例子中,"嵌入向量"都是行向量,列方向指向句子长度延伸方向
Multi-Head Attention:多头注意力机制,由多个 self-attention 模块堆叠组成
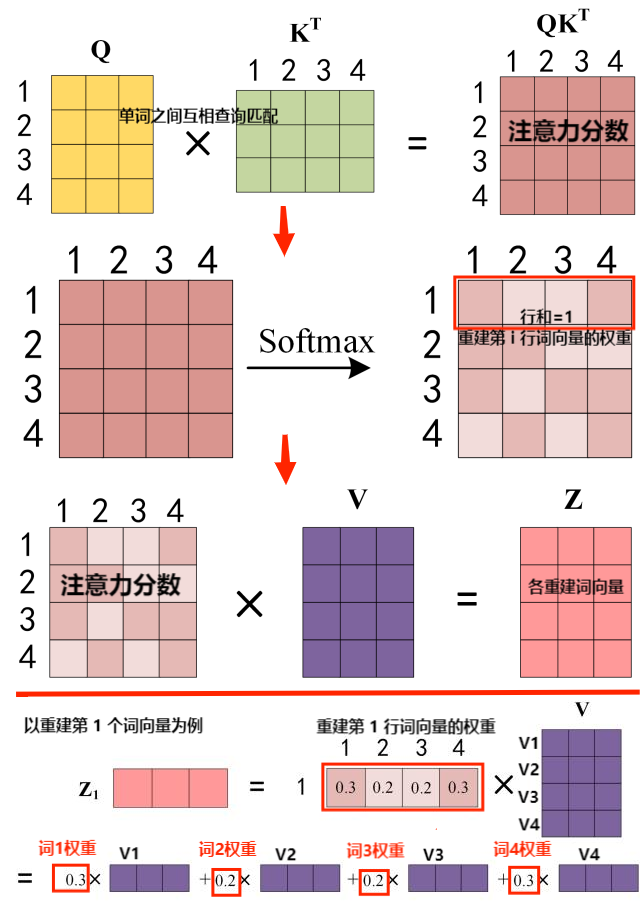
self-attention 计算公式:设 \(d_k\) 是每个 \(\text{k}\) 的维度,则有 \[ \text{attention}(\text{Q}, \text{K}, \text{V}) = \text{softmax}(\dfrac{\text{QK}^T}{\sqrt{d_k}})\text{V} \]
注意:对 \(\text{QK}^T\) 除以 \(\sqrt{d_k}\) 是为了缩小方差,从而避免让 softmax 矩阵元素间差距过大
注意力分数:设单词 1 发起的"查询"为 \(q_1\),单词 2 的"回应"为 \(k_2\),则注意力分数 \(\alpha_{1,2} = q_1 \cdot k_2^T\)
写成矩阵形式,则有 \(\alpha = \text{QK}^T\);再经过 \(\text{softmax}\) 变换(压缩归一化),使 \(\alpha\) 每一行的行和为 1
注意:"自主意"指的是单词的query同时也询问了自己的key,从而输出自己的重构信息,修正原有信息
多头注意力组合:由上述注意力模块连接堆叠得到,论文中设计了 \(h = 8\) 个注意力头,则有 \[ \begin{align} \text{MultiHead}(\text{Q}, \text{K}, \text{V}) &= \text{Concat}(\text{head}_1, \dots ,\text{head}_h)\text{W}^O \\ \text{其中 }\text{head}_i &= \text{Attention}(\text{QW}_i^\text{Q}, \text{KW}_i^\text{K}, \text{VW}_i^\text{V}) = \text{Z}_i \end{align} \] 将所有的 \(\text{Z}_i\) 拼在一起后再乘以矩阵 \(\text{W}^O\),可以得到与 \(\text{Q,K,V}\) 相同尺寸的输出矩阵 \(\text{Z}\)
多头注意力机制可以捕捉到序列内不同单词间的多种相关性(一对 \(\text{W}_i^\text{Q}, \text{W}_i^{\text{K}}\) (\(1 \le i \le h\))代表一种相关性)
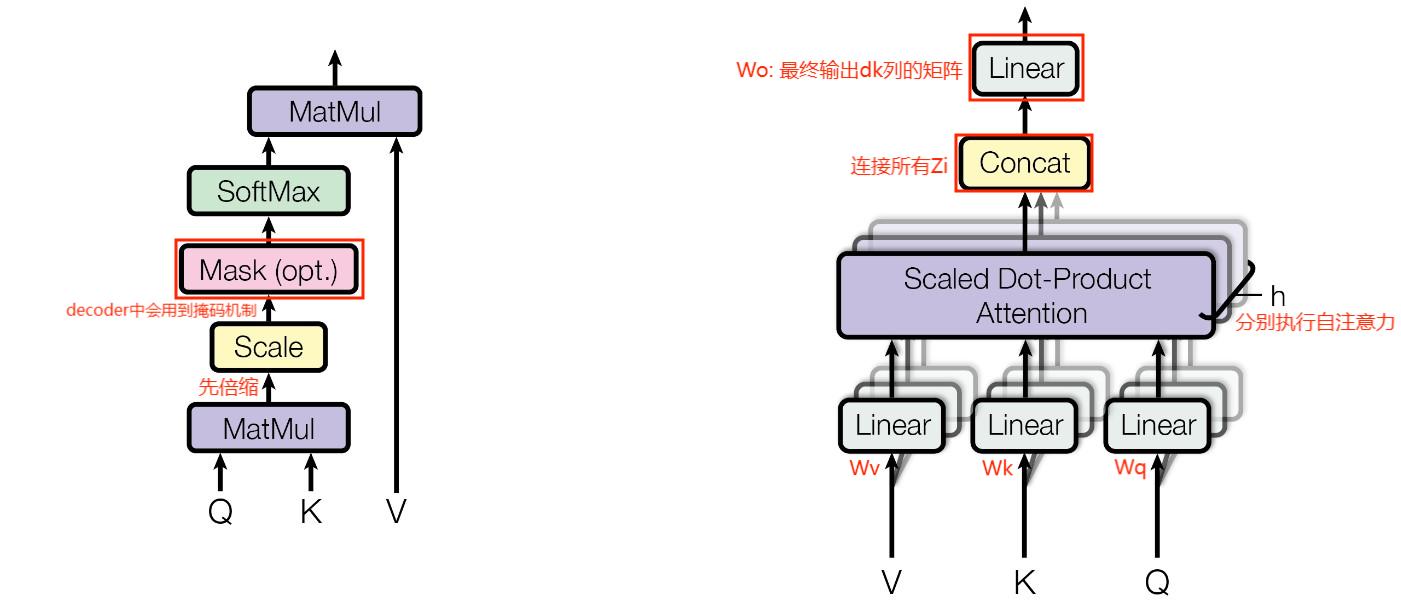
Masked Multi-Head Attention:位于 decoder 的第一层,基于掩码的多头注意力机制
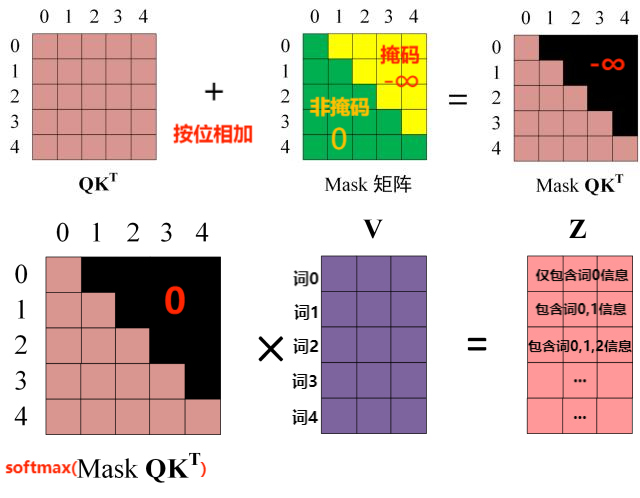
什么是"掩码":可理解成一种 0~1 矩阵,与注意力分数 \(\text{QK}^T\) 同一尺寸,可屏蔽未来的词向量信息
掩码的作用:让 decoder 在生成第 i 个单词时,只能参考前 i 个输入单词的信息("look ahead mask")
注意:decoder 是 auto-regressive 的,其输入是截至上一时间步的输出,输出下一个单词
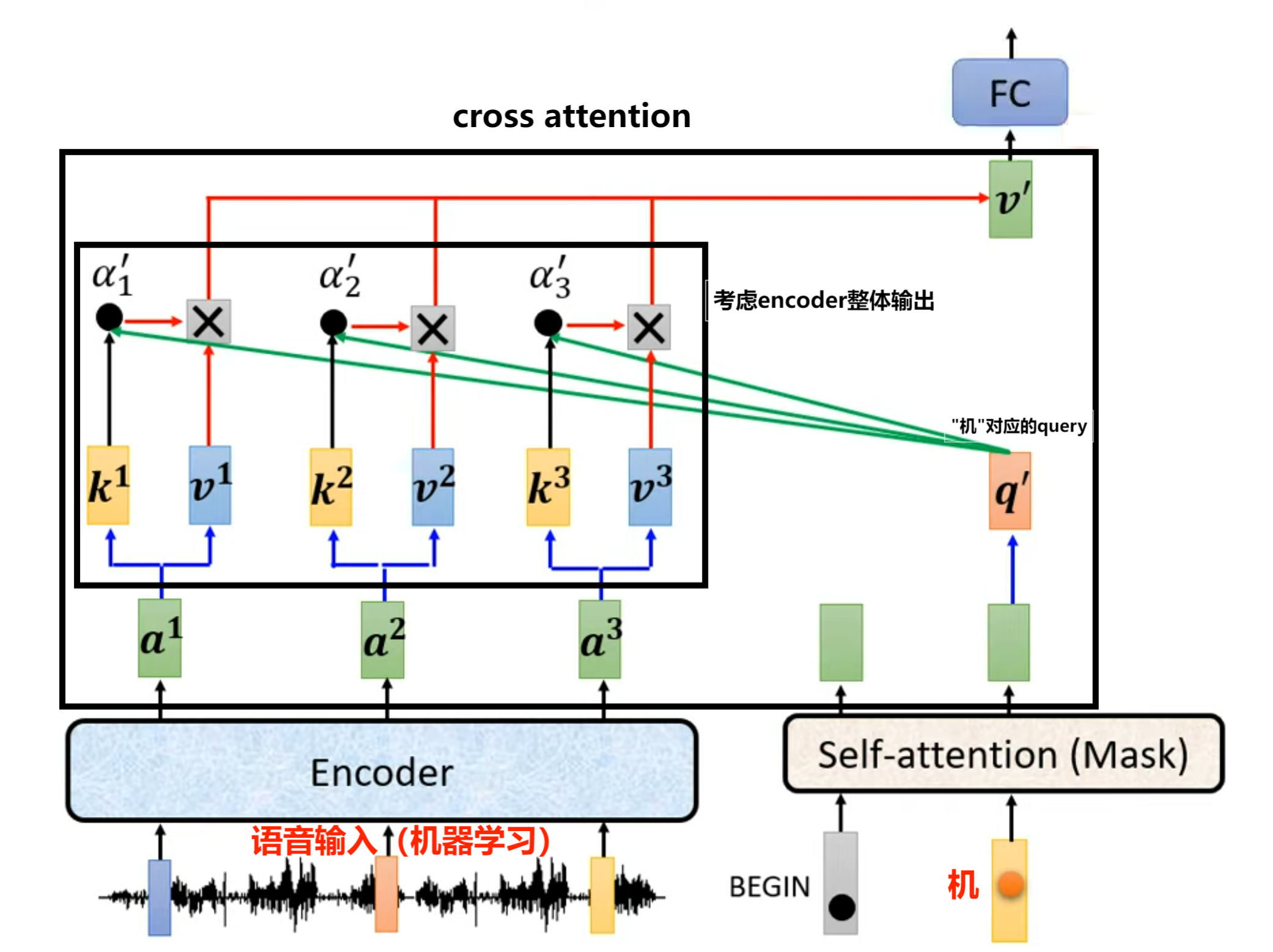
Cross Attention:位于 decoder 的第二层,其结构与 Multi-Head Attention 相同,但输入源不同
输入:输入的 \(\text{Q}\) 来自 decoder 上层 Mask Attention 模块,输入的 \(\text{K, V}\) 来自 encoder 的全局输出
输出:经过 \(\text{FFN}\)、\(\text{Linear}\)层 和 \(\textbf{softmax}\) 后,得到词表中每个单词的预测prob
注意:"交叉"是指 decoder 持有当前输出,询问已知整个序列信息的 encoder "下一个单词应该是什么?"
五、FFN 与 Add&Norm
前馈神经网络:encoder 和 decoder 中的两层非线性层,分别独立作用于序列中每个单词位置 \[ \begin{align} \text{FFN}(x) &= \text{ReLU}(x\text{W}_1 + b_1)\text{W}_2 + b_2 \\ \text{其中 ReLU}(x) &= \max(0, x) \end{align} \]
注意:FFN 是 "position-wise" 的,其输入的张量维度是 (batch_size, d_model),即独立地作用在句子中的每个位置上
\(\text{Add}\&\text{Norm}\):残差与层归一化
- 残差连接:attention 模块的输出直接与其输入相加,保留原始的序列信息
- 层归一化:常用于序列任务中,对每个样本内部的各特征进行归一化
注意:相较于"批归一化",层归一化仅作用于单一样本,不受批次大小影响,故适合处理不定长的序列任务
六、复杂度分析
- 自注意力机制:设 \(n\)
是序列长度、\(d\) 是模型表示的嵌入维度
- 每一层的复杂度:\(\mathcal{O}(n^2d)\),\(n^2\) 表示对序列内部的所有单词两两求相似度,\(d\) 表示相似度计算
- 顺序操作复杂度:\(\mathcal{O}(1)\),因为自主意力机制可以并行计算序列内所有元素之间的相似度
- 最大路径长度:\(\mathcal{O}(1)\),因为任意输出表示向量都可以直接使用所有输入单词计算得到,没有中间步骤