『machine vision-2』camera geometry

摄像机几何

一、有限摄像机

基本针孔模型：描述空间点到一张平面的中心投影
- 投影中心与主平面：
  - 摄像机中心：即投影中心，又称光心，埋藏于摄像机最内部
  - 主平面：过摄像机中心且平行于图像平面的平面
- 主轴与主点：
  - 主轴：摄像机中心到图像平面的垂直射线
  - 主点：主轴与图像平面的交点
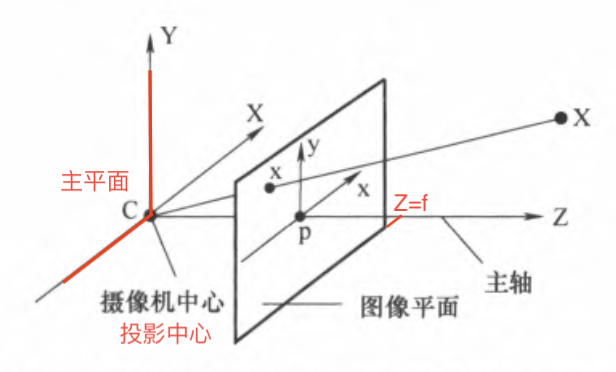
- 世界坐标到图像坐标：设空间坐标 $\textbf{X} = (\text{X}, \text{Y}, \text{Z})^T$，图像平面 $\textbf{Z} = f$，则 $\text{IR}^3 \rightarrow \text{IR}^2$ 的中心投影是： \[ \begin{align} (\text{X}, \text{Y}, \text{Z})^T \vdash (f\dfrac{\text{X}}{\text{Z}}, f\dfrac{\text{Y}}{\text{Z}})^T \end{align} \] 若用齐次坐标表示世界和图像点，则中心投影可表示为齐次坐标之间的线性映射： \[ \begin{align} \begin{bmatrix} \text{X} \\ \text{Y} \\ \text{Z} \\ 1 \end{bmatrix}\vdash \begin{bmatrix} f\text{X} \\ f\text{Y} \\ \text{Z} \end{bmatrix} = \begin{bmatrix} f & & & 0 \\ & f & & 0 \\ & & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \text{X} \\ \text{Y} \\ \text{Z} \\ 1 \end{bmatrix} \end{align} \] 可根据上式导出摄像机投影矩阵 $\text{P}$： \[ \begin{align} \text{P} = \begin{bmatrix} f & & & 0 \\ & f & & 0 \\ & & 1 & 0\end{bmatrix} = \text{diag}(f, f, 1)\text{ }[\text{I} | \textbf{0}] \end{align} \] 记图像点坐标点为三维齐次向量 $\textbf{x}$，则中心投影可简写为 $\textbf{x} = \text{P}\textbf{X}$
  
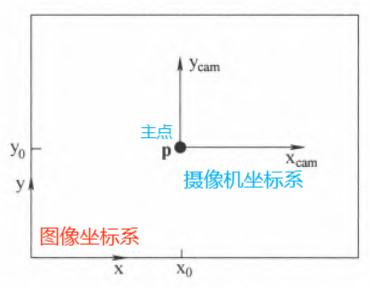
  进一步地，若主点不与图像平面的坐标原点重合（主点偏置），则一般的映射为： \[ \begin{align} &\begin{bmatrix} \text{X} \\ \text{Y} \\ \text{Z} \\ 1 \end{bmatrix} \vdash \begin{bmatrix} f{\text{X}} + \text{Z}p_x \\ f \text{Y} + \text{Z}p_y \\ \text{Z} \end{bmatrix} = \begin{bmatrix} f& & p_x & 0 \\ & f & p_y & 0 \\ & & 1 & 0 \end{bmatrix} \begin{bmatrix} \text{X} \\ \text{Y} \\ \text{Z} \\ 1 \end{bmatrix} \\ &\text{其中 }(p_x, p_y)^T \text{ 为相机主点在图像坐标系下的坐标} \end{align} \] 可根据上式导出摄像机标定矩阵 $\text{K}$（内参矩阵）： \[ \begin{align} \text{K} = \begin{bmatrix} f & & p_x \\ & f & p_y \\ & & 1 \end{bmatrix} \end{align} \] 则一般的相机映射可写为 $\textbf{x} = \text{P}\textbf{X}_\text{cam} = \text{K}[ \ \text{I}\ | \ \textbf{0} \ ]\textbf{ X}_{\text{cam}}$
  
  注意：$\textbf{X}_\text{cam}$ 表示相机坐标系与欧氏坐标系重合，与世界坐标系下的 $\textbf{X}$ 表示同一个点
  
  摄像机平移与旋转：设 ${\textbf{X}}_\text{cam}$ 表示点在相机坐标系下的齐次坐标，${\textbf{X}}$ 表示同一点在世界坐标系下的齐次坐标，由坐标系转换公式： \[ \begin{align} \textbf{X}_\text{cam} = \begin{bmatrix} \text{R} & -\text{R}\tilde{\textbf{C}} \\ \textbf{0}^T & 1 \end{bmatrix} \begin{bmatrix} \text{X} \\ \text{Y} \\ \text{Z} \\ 1 \end{bmatrix} = \begin{bmatrix} \text{R} & -\text{R}\tilde{\textbf{C}} \\ \textbf{0}^T & 1 \end{bmatrix} \textbf{ X} \end{align} \] 其中 $\text{R}_{3\times3}$ 是旋转矩阵，$\tilde{\textbf{C}}_{3\times1}$ 表示摄像机中心在世界坐标系下的非齐次坐标
  
  与一般的相机映射公式结合，可简写为 $\textbf{x} = \text{P}\textbf{X} = \text{K}\text{R} \ [ \ \text{I}\ | -\tilde{\textbf{C }}]\textbf{X}$
  - 相机内参：包含在 $\text{K}$ 中的 3 个元素中，即 $f, p_x, p_y$
  - 相机外参：包含在 $\text{R}$ 和 $\tilde{\textbf{C}}$ 的元素中，描述相机在世界坐标系下的位姿
  如果记 $\textbf{t} = -\text{R}\tilde{\textbf{C}}$，则摄像机矩阵可进一步简写为 $\text{P} = \text{K}[\text{ R }|\textbf{ t }]$ ⭐
  
  注意：$\text{P} = \text{KR}[\text{ I } | -\tilde{\textbf{C}}]$ 有 9 个自由度，其中 3 个来自 $\text{K}$、3 个来自 $\text{R}$、3 个来自 $\tilde{\text{C}}$
- CCD摄像机：一种带有电荷耦合器件的数码相机，其特点在于像素可能不是正方形
  - 图像坐标以像素数量衡量：设在 $x$ 和 $y$ 方向上的图像坐标单位距离的像素数分别为 $m_x, m_y$，则： \[ \begin{align} \text{K} = \begin{bmatrix} fm_x & & m_xp_x \\ & fm_y & m_yp_y \\ & & 1 \end{bmatrix} \end{align} \] 即借助 $m$ 将焦距和相机主点坐标转换为像素量纲 $\Rightarrow$ CCD相机有 9 + 1 = 10 个自由度
- 有限射影摄像机：在标定矩阵 $\text{K}$ 中进一步新增扭曲参数$s \ne 0$： \[ \begin{align} \text{K} = \begin{bmatrix} fm_x & s & m_xp_x \\ & fm_y & m_yp_y \\ & & 1 \end{bmatrix} \end{align} \]
  - $(\text{KR})_{3\times 3}$ 是非奇异的 $\Leftrightarrow$ $\text{P}_{3\times 4}$ 是某个有限射影摄像机的摄像机矩阵
  - 有限射影摄像机的自由度 = 12 - 1 = 11
  - 令 $\text{M} = \text{KR}$，其中 $\text{K}$ 是上三角矩阵、$\text{R}$ 是旋转矩阵，则 $\text{P} = \text{M}[\text{ I } | \text{ M}^{-1}\textbf{p}_4]$，其中 $\textbf{p}_4$ 是 $\text{P}$ 的第四列

二、射影摄像机

摄像机的构造：一般射影摄像机可按 $\text{P} = [\text{ M }| \textbf{ p}_4]$ 分块
- 摄像机中心：记作 $\textbf{C}_{4\times1}$，且总是满足 $\text{P}\textbf{C} = 0$（$\textbf{C}$ 生成了 $\text{P}$ 的 1 维右零空间）
- 列向量：设 $\text{P} = [\textbf{p}_1, \textbf{p}_2, \textbf{p}_3, \textbf{p}_4]$，其中 $\textbf{p}_i$ 是 $\text{P}$ 的第 $i$ 列，表示图像平面上特殊点的齐次坐标
  - $\textbf{p}_1, \textbf{p}_2, \textbf{p}_3$ 分别是世界坐标轴 $\text{X}, \text{Y}, \text{Z}$ 三个轴在图上的消影点，例如 $\textbf{p}_1 = \text{P }(1, 0, 0, 0)^T$
  - $\textbf{p}_4$ 是世界坐标系原点的图像点
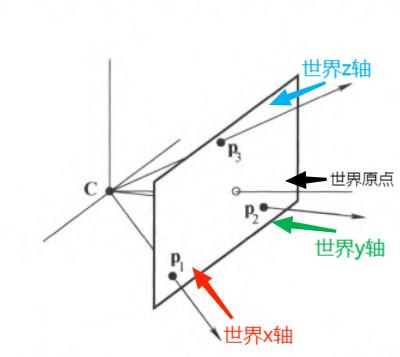
- 行向量：将 $\text{P}$ 写成行向量分块的形式，其中 $\textbf{P}^{iT}_{1\times4}$ 是 $\text{P}$ 的第 $i$ 行，表示特殊的世界平面 \[ \begin{align} \text{P} = \begin{bmatrix} \textbf{P}^{1T} \\ \textbf{P}^{2T} \\ \textbf{P}^{3T} \end{bmatrix} \end{align} \]
  - 主平面：过摄像机中心并平行于图像平面的平面；点 $\textbf{X}$ 主平面上 $\Leftrightarrow$ $\textbf{P}^{3T}\textbf{X} = 0$，即 $\text{P}^3$ 是主平面的齐次列向量表示
  - 轴平面：两个轴平面 + 一个主平面相交得到 $\textbf{C}$
    - $\textbf{C}$ 和图像$y$轴定义的平面：平面 $\textbf{P}^1$，证明如下
      - 平面 $\text{P}^{1}$ 上的点 $\textbf{X}$ 满足 $\textbf{P}^{1T} \textbf{X} = 0$ $\Rightarrow$ $\textbf{X}$ $\vdash$ $\text{P}\textbf{X} = (0, y, \omega)^T$，即被映射到图像$y$轴上
      - $\text{P}\textbf{C} = 0$ $\Rightarrow$ $\textbf{P}^{1T} \textbf{C}= 0$，即 $\textbf{C}$ 也在平面 $\textbf{P}^1$ 上
    - $\textbf{C}$ 和图像$x$轴定义的平面：平面 $\textbf{P}^2$，证明类似上面情形
    注意：轴平面 $\textbf{P}^1$ 和轴平面 $\textbf{P}^2$ 的交线是连接 $\textbf{C}$ 和图像原点的直线，一般不与相机主轴重合
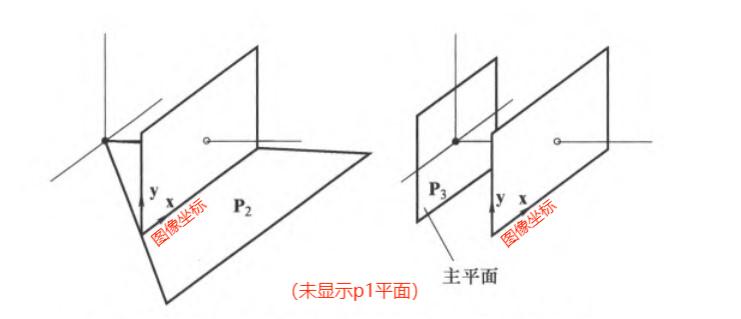
- 主点：主轴与图像平面相交于主点
  - 主点所在射线：由主平面 $\textbf{P}^3 = (p_{31}, p_{32}, p_{33}, p_{34})^T$ 可知，垂直于主平面的无穷远点为 $(p_{31}, p_{32}, p_{33}, 0)^T$
  - 主点计算公式：将上述无穷远点映射回图像平面上，即 $\text{P }(p_{31}, p_{32}, p_{33}, 0)^T$；或表示成 $\text{M}\textbf{m}^3$，其中 $\textbf{m}^{3T}$ 是 $\text{M}$ 的第三行
- 主轴向量：$\textbf{v} = |\text{M}|\textbf{m}^3$ 是主轴方向上指向摄像机前方的向量
射影摄像机对点的作用：
- 正向投影：设无穷远平面上的消影点 $\textbf{D} = (\textbf{d}^T, 0)^T$，则这些点被映射到图像上 $\textbf{x} = \text{P}\textbf{D} = [\text{ M } | \textbf{ p}_4 ]\textbf{ D} = \text{M}\textbf{d}$
- 点到射线的反向投影：给定图像上一点 $\textbf{x}$，求解空间中哪些点被映射到 $\textbf{x}$
  - 矩阵的伪逆：$\text{P}^+ = \text{P}^T (\text{PP}^T)^{-1}$，并满足 $\text{PP}^+ = \text{I}$；由 $\text{P}(\text{P}^+\textbf{x}) = \text{I}\textbf{x} = \textbf{x}$ 知，$\text{P}^+\textbf{x}$ 投影到图像的$\textbf{x}$ 上
  - 反向投影：原空间点 $\textbf{X}$ 必存在于 $\textbf{C}$ 到 $\text{P}^+\textbf{x}$ 的射线上，即原$\textbf{X}(\lambda) = \text{P}^+\textbf{x} + \lambda\textbf{C}$
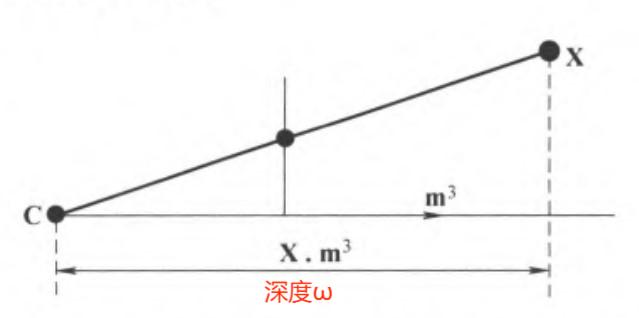
点的深度：指主平面前或后的一个空间点到主平面的距离
- 记号：设空间中某点为 $\textbf{X} = (\text{X}, \text{Y},\text{Z},1)$，投影到图像中 $\textbf{x} = \omega(x, y, 1)^T$；$\textbf{m}^3$ 表示 $\text{M}$ 的第 3 列（即主射线方向）
- 两个结论：第一个是非归一化版本、第二个是归一化版本
  - 若 $\text{P}(\text{X}, \text{Y}, \text{Z}, \text{T})^T = \omega (x, y, 1)^T$，则有向深度 $\text{depth}(\textbf{X}; \text{P}) = \dfrac{\text{sign}(\det{\text{M}}) \ \omega}{\text{T} ||\textbf{m}^3||}$
  - 若 $\text{P}(\text{X}, \text{Y}, \text{Z}, \text{1})^T = \omega (x, y, 1)^T$，并归一化使 $||\textbf{m}^3|| = 1$ 且 $\det{\text{M}} > 0$，则深度 $\text{depth}(\textbf{X}; \text{P}) = \omega$
- "归一化"版本推导：设摄像机矩阵 $\text{P} = [\text{ M } | \textbf{ p}_4]$，把三维点 $\textbf{X} = (\text{X}, \text{Y}, \text{Z}, 1)^T = (\tilde{\textbf{X}}^T, 1)^T$ 投影到图像点 $\textbf{x} = \omega (x, y, 1)^T$
  1. 投影关系为 $\textbf{x} = \text{P}\textbf{X}$；设 $\textbf{C} = (\tilde{\textbf{C}}, 1)^T$，由 $\textbf{P}^{3T}\textbf{C} = 0$ 知，$\omega = \textbf{P}^{3T}\textbf{X} = \textbf{P}^{3T}(\textbf{X} - \textbf{C})$
  2. 由 $\textbf{P}^{3T}(\textbf{X} - \textbf{C}) = \textbf{m}^{3T} (\tilde{\textbf{X}} - \tilde{\textbf{C}})$，$\omega = \textbf{P}^{3T}(\textbf{X} - \textbf{C}) = \textbf{m}^{3T} (\tilde{\textbf{X}} - \tilde{\textbf{C}})$ 为主射线与C到X的射线的点乘
  3. 若摄像机矩阵 $\text{P}$ 已被归一化使得 $\det{\text{M}} > 0$ 且 $||\textbf{m}^3|| = 1$，则 $\omega$ 可解释为 $\textbf{X}$ 到 $\textbf{C}$ 的深度
摄像机矩阵的分解：根据射影摄像机矩阵 $\text{P}$，求解摄像机的各个参数
- 摄像机中心 $\textbf{C}$：设 $\textbf{C} = (\text{X}, \text{Y}, \text{Z}, \text{T})^T$，可根据 $\text{P} = [\textbf{p}_1, \textbf{p}_2, \textbf{p}_3, \textbf{p}_4]$ 计算 $\textbf{C}$ 的各分量
  - $\text{X} = \det{([\textbf{p}_2, \textbf{p}_3, \textbf{p}_4])}$
  - $\text{Y} = -\det{([\textbf{p}_1, \textbf{p}_3, \textbf{p}_4])}$
  - $\text{Z} = \det{([\textbf{p}_1, \textbf{p}_2, \textbf{p}_4])}$
  - $\text{T} = -\det{([\textbf{p}_1, \textbf{p}_2, \textbf{p}_3])}$
- 摄像机内外参 $\text{KR}$：设 $\text{P} = [\text{ M } | -\text{M}\tilde{\textbf{C}} \ ]$，利用RQ分解可将 $\text{M}$ 分解成 $\text{M} = \text{KR}$，其中 $\text{K}$ 是上三角阵
  - RQ分解：将 $3\times 3$ 矩阵分解为上三角矩阵 * 旋转矩阵
    - 三维 Givens 旋转： $\text{Q}_x,\text{Q}_y, \text{Q}_z$ 分别是绕 $x, y, z$ 轴转的旋转矩阵
    - 用 Givens 旋转将 $\text{A}_{3\times 3}$ 进行 RQ分解：$\text{A} = \text{RQ}$，其中 $\text{Q} = \text{Q}_z^T\text{Q}_y^T\text{Q}_x^T$ 是旋转矩阵，$\text{R}$ 是上三角阵
  - 有关扭曲参数 $s$：常在对照片拍照时发生，即"二次取像"，这将导致 $\text{K}$ 中的 $s \ne 0$

三、无穷远摄像机

仿射摄像机：$\text{P}$ 的最后一行形如 $\textbf{P}^{3T} = (0, 0, 0, 1)$，主平面距离距离世界坐标系无穷远（透视效果随之消失）
- 用有限摄像机模拟仿射摄像机：不断增加焦距，同时让摄像机远离物体，透视效果便会消失
  1. 设初始摄像机矩阵为 $\text{P}_0$，同有限摄像机 \[ \begin{align} \text{P}_0 &= \text{KR}[\text{ I } | -\tilde{\textbf{C}} \ ] \\ &=\text{K}\begin{bmatrix} \textbf{r}^{1T} & -\textbf{r}^{1T}\tilde{\textbf{C}} \\ \textbf{r}^{2T} & -\textbf{r}^{2T}\tilde{\textbf{C}} \\ \textbf{r}^{3T} & -\textbf{r}^{3T}\tilde{\textbf{C}} \end{bmatrix} \end{align} \] 其中 $\textbf{r}^{iT}$ 是旋转矩阵的第 $i$ 行，是摄像机的定向；设 $d_0 = -\textbf{r}^{3T}\tilde{\textbf{C}}$ 是世界原点到相机中心在主射线方向上的距离
  2. 设相机在 $t$ 时间内以单位速度沿主射线向后移动：将 $\tilde{\textbf{C}}$ 代替为 $\tilde{\textbf{C}} - t\textbf{r}^3$ 可得到 $\text{P}_t$ \[ \begin{align} \text{P}_t = \text{K}\begin{bmatrix} \textbf{r}^{1T} & -\textbf{r}^{1T}\tilde{\textbf{C}} \\ \textbf{r}^{2T} & -\textbf{r}^{2T}\tilde{\textbf{C}} \\ \textbf{r}^{3T} & -\textbf{r}^{3T}\tilde{\textbf{C}} + t \end{bmatrix} \end{align} \] 设 $d_t = \textbf{r}^{3T}\tilde{\textbf{C}} + t$ 是 $t$ 时刻世界原点到相机中心在主射线方向上的距离
  3. 合成追踪变焦不变效果：假定使图像大小保持不变的放大因子是 $k = \dfrac{d_t}{d_0}$ \[ \begin{align} \text{P}_t = \text{K}\begin{bmatrix} \dfrac{d_t}{d_0} & & \\ & \dfrac{d_t}{d_0} & \\ & & 1 \end{bmatrix} \begin{bmatrix} \textbf{r}^{1T} & -\textbf{r}^{1T}\tilde{\textbf{C}} \\ \textbf{r}^{2T} & -\textbf{r}^{2T}\tilde{\textbf{C}} \\ \textbf{r}^{3T} & d_t \end{bmatrix} = \dfrac{d_t}{d_0} \text{K} \begin{bmatrix} \textbf{r}^{1T} & -\textbf{r}^{1T}\tilde{\textbf{C}} \\ \textbf{r}^{2T} & -\textbf{r}^{2T}\tilde{\textbf{C}} \\ \textbf{r}^{3T} \dfrac{d_0}{d_t} & d_0 \end{bmatrix} \end{align} \] 忽略前面的 $\dfrac{d_t}{d_0}$ 因子，可得到最终的 $\text{P}_t$ 为： \[ \begin{align} \text{P}_t = \text{K} \begin{bmatrix} \textbf{r}^{1T} & -\textbf{r}^{1T}\tilde{\textbf{C}} \\ \textbf{r}^{2T} & -\textbf{r}^{2T}\tilde{\textbf{C}} \\ \textbf{r}^{3T} \dfrac{d_0}{d_t} & d_0 \end{bmatrix} \end{align} \] 可验证当 $t = 0$ 时，$\text{P}_t = \text{P}_0$；令相机远离物体无穷远，即 $d_t \rightarrow \infty$ ，可得到 $\text{P}_{\infty}$： \[ \begin{align} \text{P}_{\infty} = \lim_{t\rightarrow \infty}\text{P}_t = \text{K}\begin{bmatrix} \textbf{r}^{1T} & -\textbf{r}^{1T}\tilde{\textbf{C}} \\ \textbf{r}^{2T} & -\textbf{r}^{2T}\tilde{\textbf{C}} \\ \textbf{0}^T & d_0 \end{bmatrix} \end{align} \] 可见 $\text{P}_{\infty}$ 的最后一行的前三个元素 = 0；由仿射摄像机定义，$\text{P}_{\infty}$ 是仿射摄像机
仿射摄像机误差：设 $\alpha, \beta \in \mathbb{R}$；由于 $\textbf{r}^{3}$ 表示相机主轴方向，故在过世界原点并垂直于 $\textbf{r}^3$ 的平面上的任何点 $\textbf{X}$ 为 \[ \begin{align} &\textbf{X} = \begin{bmatrix} \alpha \textbf{r}^1 + \beta \textbf{r}^2 \\ 1 \end{bmatrix} \\ \end{align} \] 由于 $\textbf{r}^{3T}(\alpha \textbf{r}^1 + \beta \textbf{r}^2) = 0$，故 $\text{P}_0 \textbf{X} = \text{P}_t\textbf{X} = \text{P}_t \textbf{X}$ 恒成立

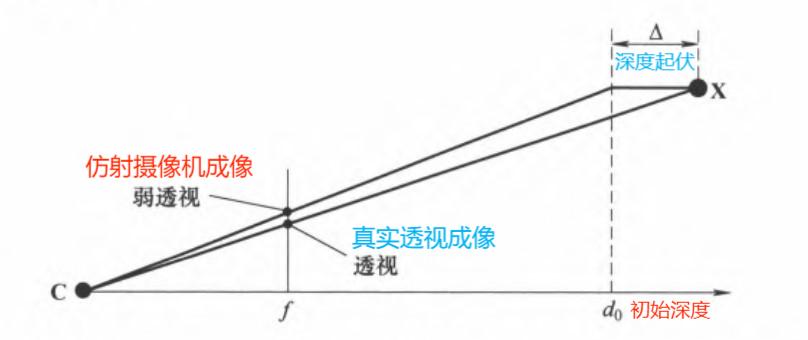
假设某个点 $\textbf{X}$ 距离上述平面距离 $\Delta$，则点 $\textbf{X}$ 可表示为： \[ \begin{align} \textbf{X} = \begin{bmatrix} \alpha \textbf{r}^1 + \beta \textbf{r}^2 + \Delta \textbf{r}^3 \\ 1 \end{bmatrix} \end{align} \] 同时被摄像机 $\text{P}_0$ 和 $\text{P}_{\infty}$ 分别投影到图像上的点 $\textbf{x}$： \[ \begin{align} \textbf{x}_{\text{proj}} = \text{P}_0 \textbf{X} = \text{K}\begin{bmatrix} \alpha - \textbf{r}^{1T} \tilde{\textbf{C}} \\ \beta - \textbf{r}^{2T} \tilde{\textbf{C}} \\ d_0 + \Delta \end{bmatrix} = \text{K}\begin{bmatrix} \tilde{x} \\ \tilde{y} \\ d_0 + \Delta \end{bmatrix} \quad \textbf{x}_{\text{affine}} = \text{P}_{\infty}\textbf{X} = \text{K}\begin{bmatrix} \alpha - \textbf{r}^{1T} \tilde{\textbf{C}} \\ \beta - \textbf{r}^{2T} \tilde{\textbf{C}} \\ d_0 \end{bmatrix} = \text{K}\begin{bmatrix} \tilde{x} \\ \tilde{y} \\ d_0 \end{bmatrix} \end{align} \] 设图像平面上的主点的非齐次坐标为 $\tilde{\textbf{x}}_0$，则新的标定矩阵 $\text{K}$ 和图像映射点 $\textbf{x}$ 分别为： \[ \begin{align} &\text{内参矩阵 }\text{K} = \begin{bmatrix} \text{K}_{2\times 2} & \tilde{\textbf{x}}_0 \\ \tilde{0}^T & 1 \end{bmatrix} \text{（其中 }\text{K}_{2\times 2} \text{ 为上三角方阵）} \\ &\text{图上映射点 }\textbf{x}_{\text{proj}} = \begin{bmatrix} \text{K}_{2\times 2} \tilde{\textbf{x}} + (d_0 + \Delta)\tilde{\textbf{x}}_0 \\ d_0 + \Delta \end{bmatrix} = \begin{bmatrix} \tilde{\textbf{x}}_{\text{proj}} \\ d_0 + \Delta \end{bmatrix} \\ & \qquad \ \ \quad \quad \ \textbf{x}_{\text{affine}} = \begin{bmatrix} \text{K}_{2\times 2} \tilde{\textbf{x}} + d_0\tilde{\textbf{x}}_0 \\ d_0 \end{bmatrix} = \begin{bmatrix} \tilde{\textbf{x}}_{\text{affine}} \\ d_0 \end{bmatrix} \end{align} \] 通过消元可得到 $\tilde{\textbf{x}}_{\text{proj}}$ 和 $\tilde{\textbf{x}}_{\text{affine}}$ 之间的关系： \[ \begin{align} &\tilde{\textbf{x}}_{\text{affine}} - \tilde{\textbf{x}}_{0} = \dfrac{d_0 + \Delta}{d_0} (\tilde{\textbf{x}}_{\text{proj}} - \tilde{\textbf{x}}_0) \\ \end{align} \] 上式表明用 $\text{P}_{\infty}$ 近似 $\text{P}_0$ 的效果是：在图像平面上使 $\tilde{\textbf{x}}$ 远离（或靠近）主点 $\tilde{\textbf{x}}_0$，移动因子为 $\dfrac{d_0 + \Delta}{d_0}$

注意：由上述关系知，若深度起伏 $\Delta$ 相对初始深度 $d_0$ 较小，则用仿射摄像机可较好地逼近真实的透视图像
仿射摄像机的分解：仿射摄像机的摄像机矩阵 $\text{P}$ 可表示为： \[ \begin{align} \text{P}_{\infty} = \begin{bmatrix} \text{K}_{2\times 2} & \tilde{\textbf{x}}_0 \\ \hat{\textbf{0}}^T & 1 \end{bmatrix} \begin{bmatrix} \hat{\text{R}} & \hat{\textbf{t}} \\ \textbf{0}^T & d_0 \end{bmatrix} \end{align} \] 其中 $\hat{\text{R}}_{2\times 3}$ 由旋转矩阵的前两行组成，$\hat{\textbf{t}} = (-\textbf{r}^{1T}\tilde{\textbf{C}}, -\textbf{r}^{2T}\tilde{\textbf{C}})^T$，$ = (0, 0)^T $；令 $\tilde{\textbf{x}}_0 = \textbf{0}$，并设 $d_0 = 1$： \[ \text{P}_{\infty} = \begin{bmatrix} \text{K}_{2\times 2} & \hat{\textbf{0}} \\ \hat{\textbf{0}}^T & 1 \end{bmatrix} \begin{bmatrix} \hat{\text{R}} & \hat{\textbf{t}} \\ \textbf{0}^T & 1 \end{bmatrix} \]

注意：若令 $\hat{\textbf{t}} = \hat{\textbf{0}}$，世界原点的图像是 $\text{P}(0, 0, 0, 1)^T = (\tilde{\textbf{x}}_0^T, 1)^T$，则相机主点 $\tilde{\textbf{x}}_0$ 就会与世界坐标的选取有关
仿射摄像机的性质：
仿射摄像机的主平面都是无穷远平面，反之同样成立
世界的平行直线被投影到图像中的平行直线（透视性质消失）

四、求解摄像机矩阵

基于"几何误差"的相机估计：设世界到图像的测量点对为 $\{\textbf{X}_i \leftrightarrow \textbf{x}_i\}$，求解最小化 $\sum_{i}d(\textbf{x}_i, \text{P}\textbf{X}_i)^2$ 的 $\text{P}$
- 所有测量点 $\textbf{X}_i$ 和 $\textbf{x}_i$ 都没有误差：
  1. 找出 $n \ge 6$ 组由世界到图像的点对 $\textbf{X}_i \leftrightarrow \textbf{x}_i$
    
    注意：之所以要找至少 6 个点对，是因为 $\text{P}$ 共有 12 个元素，抛开缩放因子共有 11dof，故需要至少 6 个点对解出 $\text{P}$
  2. 使用归一化的DLT算法求解一个 $\text{P}$ 的初始估计 $\tilde{\textbf{P}}$
    - 归一化：用某个相似变换 $\text{T}$ 归一化图像点，记 $\tilde{\textbf{x}}_i = \text{T}\textbf{x}_i$；用另一个相似变换 $\text{U}$ 归一化空间点，记 $\tilde{\textbf{X}}_i = \text{U}\textbf{X}_i$
    - DLT：将每组 $\tilde{\textbf{X}}_i \leftrightarrow \tilde{\textbf{x}}_i$ 对应的方程矩阵 $\text{A}_i$ 拼接成一个大矩阵 $\text{A}_{2n \times 12}$，
      记 $\textbf{p}$ 为 $\tilde{\textbf{P}}$ 中元素构成的向量，则 $\text{A}\textbf{p} = 0$ 的满足 $||\textbf{p}|| = 1$ 的解是 $\text{A}$ 对应于最小奇异值的单位奇异向量 \[ \begin{align} \text{A}_i\textbf{p} = \begin{bmatrix} \textbf{0}^T & -\omega_i \textbf{X}_i^T & y_i\textbf{X}_i^T \\ \omega_i \textbf{X}_i^T & \textbf{0}^T & -x_i\textbf{X}_i^T \end{bmatrix} \begin{bmatrix} \textbf{P}_1 \\ \textbf{P}_2 \\ \textbf{P}_3 \end{bmatrix} = 0 \end{align} \]
  3. 最小化几何误差：以 $\tilde{\text{P}}$ 为初始点，用迭代算法最小化几何误差 $\sum_{i}d(\tilde{\textbf{x}}_i, \tilde{\text{P}}\tilde{\textbf{X}}_i)^2$
  4. 解除归一化：把 $\tilde{\text{P}}$ 还原回 $\text{P} = \text{T}^{-1} \tilde{\textbf{P}}\text{U}$
- 仅三维点 $\textbf{X}_i$ 有测量误差：几何误差重定义为 $\sum_{i}d(\textbf{X}_i, \hat{\textbf{X}}_i)^2$，其中 $\hat{\textbf{X}}_i$ 是通过 $\text{P}\textbf{X}_i$ 准确映射到 $\textbf{x}_i$ 的最靠近 $\textbf{X}_i$ 的点
- $\textbf{X}_i$ 和 $\textbf{x}_i$ 都有测量误差：几何误差重定义为 $\sum_{i}d(\textbf{x}_i, \text{P}\hat{\textbf{X}}_i)^2 + d(\textbf{X}_i, \hat{\textbf{X}}_i)^2$，需要将所有 $\hat{\textbf{X}}_i$ 添加到参数中
仿射摄像机的估计：设世界和图像的测量点对为 $\{\textbf{X}_i \leftrightarrow \textbf{x}_i\}$，在 $\textbf{P}^{3T} = (0, 0, 0, 1)$ 的条件下最小化 $\sum_{i} d(\textbf{x}_i, \text{P}\textbf{X}_i)^2$
1. 找出 $n \ge 4$ 组由世界到图像的点对 $\textbf{X}_i \leftrightarrow \textbf{x}_i$
2. 使用归一化的DLT算法求解一个 $\text{P}$ 的初始估计 $\tilde{\textbf{P}}$
  - 归一化：分别用相似变换 $\text{T}$ 和 $\text{U}$ 归一化得到 $\tilde{\textbf{x}}_i$ 和 $\tilde{\textbf{X}}_i$，最后一个元素都是 1
  - DLT：简化上面一般形式的方程，将每组对应 $\tilde{\textbf{X}}_i \leftrightarrow \tilde{\textbf{x}}_i$ 产生的方程矩阵 $\text{A}_i$ 拼成大矩阵 $\text{A}_{2n\times 8}$
    其中 $\textbf{p}$ 指 $\tilde{\textbf{P}}$ 的前 8 个元素 \[ \begin{align} \text{A}_i \textbf{p} = \begin{bmatrix} \tilde{\textbf{X}}_i^T & \textbf{0}^T \\ \textbf{0}^T & \tilde{\textbf{X}}_i^T \end{bmatrix}\begin{bmatrix} \tilde{\textbf{P}}^1 \\ \tilde{\textbf{P}}^2 \end{bmatrix} = \begin{bmatrix} \tilde{x}_i \\ \tilde{y}_i \end{bmatrix} = \textbf{b} \end{align} \]
3. 求解 $\textbf{p} = \text{A}^+ \textbf{b}$（"+"指"伪逆"，定义见"射影摄像机"），剩下的第三行 $\tilde{\textbf{P}}^{3T} = (0, 0, 0, 1)$
4. 解除归一化：把 $\tilde{\textbf{P}}$ 还原回 $\textbf{P} = \text{T}^{-1}\tilde{\textbf{P}}\text{U}$
径向失真：随着焦距减小，图像线条出现弯曲失真
- 径向失真模型：设 $(\tilde{\textbf{x}}, \tilde{\textbf{y}})$ 是理想图像的位置（遵循线性投影），$(x_d, y_d)$ 是径向失真后的实际图像位置 \[ \begin{align} \begin{bmatrix} x_d \\ y_d \end{bmatrix} = L(\tilde{r})\begin{bmatrix} \tilde{x} \\ \tilde{y} \end{bmatrix} \end{align} \] 其中半径 $\tilde{r}$ 表示到径向失真中心的距离，$L(\tilde{r})$ 是仅关于 $\tilde{r}$ 的函数
- 失真矫正：在像素坐标系中，设 $(x, y)$ 是测量坐标，$(\hat{x}, \hat{y})$ 是矫正后的坐标，$(x_c, y_c)$ 是径向失真中心，则矫正方程为： \[ \begin{align} &\hat{x} = x_c + L(r)(x - x_c) \\ &\hat{y} = y_c + L(r)(y - y_c) \\ \end{align} \]
  - 失真中心：一般设置为相机主点
  - 失真函数：一般通过迭代优化的方式确定
    - 待优化参数：失真参数 $\mathcal{K}_i$ 和失真中心 $(x_c, y_c)$
    - 优化目标：世界场景直线的图像尽量是直线，比如最小化两像点直连线和两像中心之间的距离
    这样可得到 Taylor 展开形式的失真函数 $L(r) = 1 + \sum_{i}^N \mathcal{K}_i r^i$，且仅当 $r > 0$ 时 $L(r)$ 有定义

五、单视图几何

射影摄像机对几何体的作用：
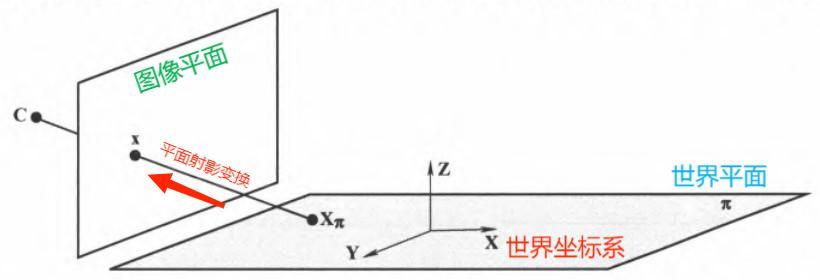
- 对平面的作用：若选择世界坐标系下的XY平面为世界平面$\pi$，则$\pi$上点的图像为： \[ \textbf{x} = \text{P}\textbf{X} = [\textbf{p}_1, \textbf{p}_2, \textbf{p}_3, \textbf{p}_4]\begin{bmatrix} \text{X} \\ \text{Y} \\ 0 \\ 1 \end{bmatrix} = [\textbf{p}_1, \textbf{p}_2, \textbf{p}_4] \begin{bmatrix}\text{X} \\ \text{Y} \\ 1 \end{bmatrix} \] 故映射 $\textbf{X}_{\pi} \rightarrow \textbf{x}$ 是一个平面射影变换 $\textbf{x} = \text{H}_{3\times3}\textbf{X}_{\pi}$，其中 $\text{H}$ 是满秩的
  
  对标定摄像机 $\text{P} = \text{K}[\text{ R }|\textbf{ t }]$，世界平面 $\text{Z} = 0$ 到图像之间的单应是 $\text{H} = \text{K}[\textbf{r}_1, \textbf{r}_2, \textbf{t}]$
  
  注意：由于能任选世界坐标系，故总是可以把世界场景中的任意平面设在 $\text{Z} = 0$ 处
- 对直线的作用：
  - 正向投影：设世界直线为 $\textbf{AB}$，其对应图像为 $\textbf{ab}$，则投影到直线 $\textbf{ab}$ 上的点 $\textbf{x}(\mu)$ 满足 \[ \begin{align} \textbf{x}(\mu) &= \text{P}(\textbf{A} + \mu \textbf{B}) = \text{P}\textbf{A} + \mu\text{P}\textbf{B} \\ &= \textbf{a} + \mu \textbf{b} \end{align} \]
  - 反向投影：经过摄像机 $\text{P}$ 映射成一条图像直线 $\textbf{I}$ 的世界空间点集合为平面 $\text{P}^T \textbf{I}$，证明过程如下： \[ \begin{align} &\text{由 }\textbf{x} \text{ 在 }\text{I} \text{ 上}\Leftrightarrow \textbf{x}^T\textbf{I} = 0 \ \text{可知，} \ \text{图像点 }\text{P}\textbf{X} \ \text{在直线 } \textbf{I} \ \text{上} \Leftrightarrow (\text{P}\textbf{X})^T \textbf{I} = \textbf{X}^T(\text{P}^T\textbf{I}) = 0 \\ &\text{若 }\text{P}^T\textbf{I} \ \text{表示一个平面，故空间点 }\textbf{X} \text{ 在该平面上}\Leftrightarrow \textbf{X }映射到图像直线 \textbf{ I }上，证毕。 \end{align} \]
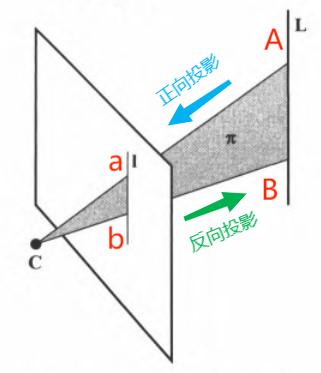
摄像机中心：为简便起见，设摄像机坐标系和世界坐标系重合，即 $\text{P} = \text{K}[\textbf{ I } | \textbf{ 0 }]$
- 焦距增加：设 $\textbf{x}$ 和 $\textbf{x}'$ 分别是点 $\textbf{X}$ 变焦前后的图像，则两个图像点满足： \[ \begin{align} &\textbf{x} = \text{K}[\textbf{ I } | \textbf{ 0 }] \textbf{X} \\ &\textbf{x}' = \text{K}'[\textbf{ I } | \textbf{ 0 }] \textbf{X} = \text{K}'(\text{K}^{-1}\text{K})[\textbf{ I } | \textbf{ 0 }]\textbf{X} \\ & \quad =\text{K}'\text{K}^{-1}(\text{K}[\textbf{ I } | \textbf{ 0 }]\textbf{X}) = \text{K}'\text{K}^{-1}\textbf{x} \\ &\text{同时说明 }\textbf{x} \text{ 和 }\textbf{x}' \text{ 之间的转换是一个平面单应，}\text{H} = \text{K}'\text{K}^{-1} \end{align} \] 由于 $\text{K}$ 和 $\text{K}'$ 之间仅有焦距不同，设 $\tilde{\textbf{x}}_0$ 为非齐次主点，$k = \dfrac{f'}{f}$ 是变焦因子，则有 \[ \begin{align} \text{K}'\text{K}^{-1} = \begin{bmatrix} k\textbf{I} & (1 - k)\tilde{\textbf{x}}_0 \\ \textbf{0}^T & 1 \end{bmatrix} \end{align} \] 上式左右同时右乘 $\text{K}$，可改写为 \[ \begin{align} \text{K}' = \begin{bmatrix} k'\textbf{I} & (1 - k)\tilde{\textbf{x}}_0 \\ \textbf{0}^T & 1 \end{bmatrix}\text{K} = \text{K}\begin{bmatrix} k\textbf{I} & \\ & 1 \end{bmatrix} \end{align} \] 故变焦因子 $k$ 的效果 $\Leftrightarrow$ 给 $\text{K}$ 右乘 $\text{diag}(k, k, 1)$
- 相机旋转：设 $\textbf{x}$ 和 $\textbf{x}'$ 分别是点 $\textbf{X}$ 旋转前后的图像，则两个图像点满足： \[ \begin{align} &\textbf{x} = \text{K}[\textbf{ I } | \textbf{ 0 }]\textbf{X} \\ &\textbf{x}' = \text{K}[\textbf{ R } | \textbf{ 0 }]\textbf{X} = \text{KRK}^{-1}\textbf{x} \\ &\text{同时说明 }\textbf{x} \text{ 和 }\textbf{x}' \text{ 之间的转换也是一个平面单应，}\text{H} = \text{KRK}^{-1} \end{align} \]
  - 旋转性质：单应 $\text{H}$ 的三个特征值为 $\{\mu, \mu e^{i\theta}, \mu e^{-i\theta}\}$，在相差一个 $\mu$ 下与 $\text{R}$ 相同
    - 旋转角度：由 $\text{H}$ 的复特征值的相位算出，也就是 $\theta$
    - 旋转轴消影点：$\text{H}$ 的实特征值对应的特征向量
  - 视图合成：由现有图像生成新的由不同摄像机定向产生的图像，算法流程如下
    1. 假设已经有一张正视图，其中世界矩形与图像矩形的长宽比相等
    2. 求解一个单应 $\text{H}$，该单应把图像中的四边形映射回具有正确长宽比的矩形
    3. 在 $\textbf{I} \rightarrow \textbf{H}$ 上进行形变插补，生成单应前后之间的一系列中间图像，囊括了不同相机视角下的图像
  - 全景拼图：将摄像机绕其中心旋转得到的一系列图像进行射影形变插补得到平面全景图
    1. 选择图像集合中的一张图像 a 作为参考图像
    2. 计算其它一幅图像 b 到参考图像的单应 $\text{H}$
    3. 用得到的 $\text{H}$ 对图像 b 进行形变插补，并用系列图像中 b 与 a 之间的非重叠部分扩大参考图像
    4. 反复执行以两步，直至所有图像处理完毕，得到全景拼图
透视消影点：一条世界直线的消影点是平行于该直线并过 $\textbf{C}$ 的射线 与 图像平面 的交点
- 求解消影点：设三维空间过点 $\textbf{A}$ 且方向为 $\textbf{D} = (\textbf{d}^T, \textbf{0})^T$ 的直线上的点为 $\textbf{X}_{\lambda} = \textbf{A} + \lambda \textbf{D}$ \[ \begin{align} &\text{在射影摄像机 }\text{P} = \text{K}[\textbf{ I } | \textbf{ 0 }] \text{ 的作用下，像点 }\textbf{x}(\lambda)\text{ 可表示为：} \\ &\textbf{x}(\lambda) = \text{P}\textbf{X}_{\lambda} = \text{P}\textbf{A} + \lambda \text{P}\textbf{D} = \textbf{a} + \lambda \text{K}\textbf{d} \end{align} \] 进而解得无穷远点 $\textbf{D}$ 的像为 $\textbf{v} = \lim_{\lambda \rightarrow \infty}\textbf{x}(\lambda) = \lim_{\lambda \rightarrow \infty}(\textbf{a} + \lambda \text{K}\textbf{d}) = \text{K}\textbf{d}$
  
  注意：由上式可知消影点仅与直线方向有关，与直线位置 $\text{A}$ 无关；同一组世界平行线有共同的消影点
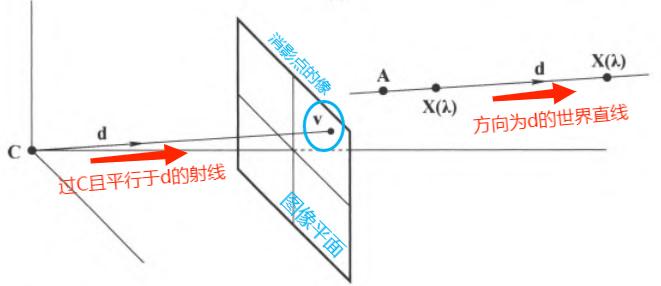
- 为什么一组世界平行线相交于图像的同一点？简便起见假设平行线都平行于主轴，原理如下图所示：
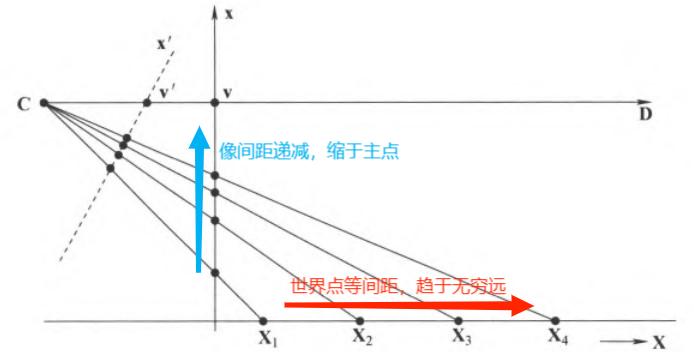
透视消影线：一条世界平面的消影平面是平行于该平面并过 $\textbf{C}$ 的平面 与 图像平面 的交线
- 由三条共面等距平行线的图像计算消影线：设该三条图像直线为 $\textbf{I}_0, \textbf{I}_1, \textbf{I}_2$，则消影线的闭形式解为： \[ \textbf{I} = ((\textbf{I}_0 \times \textbf{I}_2)^T(\textbf{I}_1\times \textbf{I}_2))\textbf{I}_1 + 2((\textbf{I}_0 \times \textbf{I}_1)^T(\textbf{I}_2 \times \textbf{I}_1))\textbf{I}_2 \]
  
  注意：这种方法常用且好用，特别适用于含窗户、栅栏、斑马线等带有典型世界平行线的图像
- 由消影线反推平面：消影线为 $\textbf{I}$ 的平面的法向为 $\textbf{n} = \text{K}^T\textbf{I}$