『machine vision-1』projective geometry
射影几何与变换
一、2D 射影几何
欧式几何与射影几何:
- 欧氏几何:描述物体角度和形状的几何,两条平行线永不相交;欧式空间记作 \(\text{IR}^n\)
- 射影几何:欧氏空间的扩展,任意两条直线都相交,两条平行直线相交于"无穷远点"(理想点)处;射影空间记作 \(\text{IP}^n\)
点与直线的表示方法:
- 直线的齐次表示:平面上的一条直线用方程 \(ax + by + c = 0\) 表示,或者用齐次向量 \(k(a, b, c)^T\) 表示
- 点的齐次表示:平面上的一个点用非齐次有序对 \((x, y)^T\) 表示,或者用齐次坐标 \(k(x, y, 1)\) 表示
注意:点 \(x\) 在平面直线 \(I\) 上 \(\Leftrightarrow\) \(x^TI = 0\),其中 \(x\) 是齐次形式的平面坐标
直线的交点 与 两点的连线:
- 直线的交点:设两条直线为 \(I\) 和 \(I'\),则 两直线的交点为 \(x = I \times I'\)
- 两点的连线:设两个点为 \(x\) 和 \(x'\),则 两点的连线为 \(I = x \times x'\)
注意:两条平行线的交点形式为 \((x, y, 0)\),其非齐次表示为 \((\dfrac{x}{0}, \dfrac{y}{0})\),可见其在 \(\text{IR}^2\) 上是无意义的
理想点:又称"无穷远点",形式为 \((x_1, x_2, 0)^T\),在"无穷远直线" \(I_{\infty} = (0, 0, 1)^T\) 上
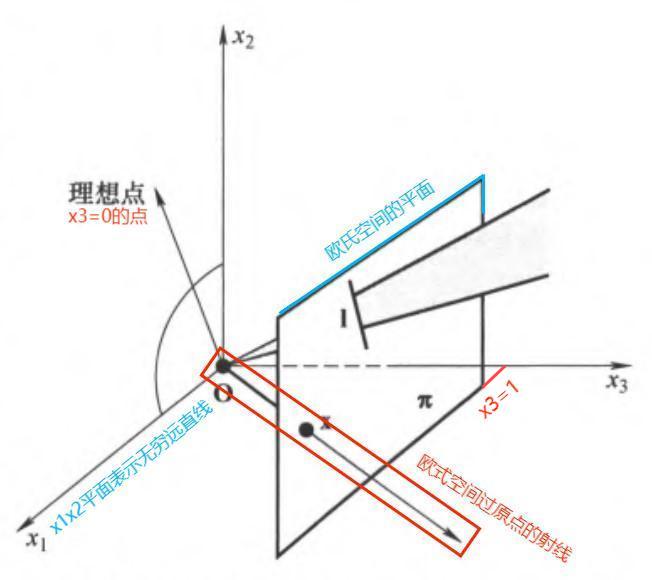
\(\text{IP}^2\) 和 \(\text{IR}^3\) 的关系:
- \(\text{IR}^3\) 中过原点的射线 \(\Rightarrow\) \(\text{IP}^2\) 中的点;当 \(k\) 变化时,向量 \(k(x_1, x_2, x_3)\) 形成一条过原点的射线
- \(\text{IR}^3\) 中过原点的平面 \(\Rightarrow\) \(\text{IP}^2\) 中的直线;两相异的 \(\text{IR}^3\) 平面交成一条射线 \(\rightarrow\) 两相异的 \(\text{IP}^2\) 直线交于一个点
注意:\(\text{IP}^2\) 中的点和直线可用 \(\text{IR}^3\) 中的平面 \(x_3 = 1\) 截取 \(\text{IR}^3\) 中的射线和平面得到,如下图所示
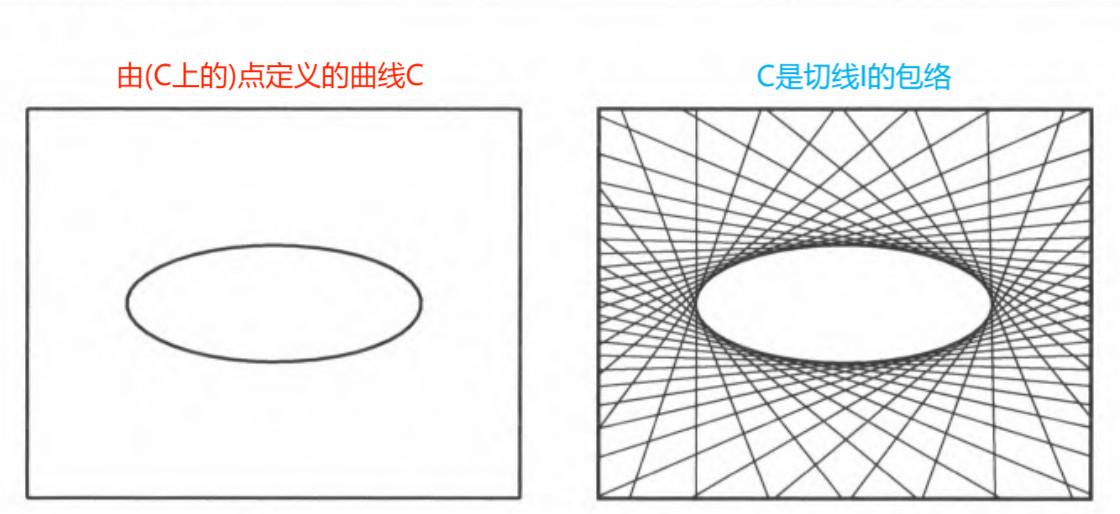
二次曲线 与 二次对偶曲线:
二次曲线的非齐次表示:\(ax^2 + bxy + cy^2 + dx + ey + f = 0\)
二次曲线的齐次表示:令 \(x \rightarrow \dfrac{x_1}{x_3}\)、\(y \rightarrow \dfrac{x_2}{x_3}\),则 \(ax_1^2 + bx_1b_2 + cx_2^2 + dx_1x_2 + ex_2 x_3 + fx_3 = 0\) \[ \begin{align} &x^T Cx = 0 \\ \text{其中 }C =& \begin{bmatrix} a & \dfrac{b}{2} & \dfrac{d}{2} \\ \dfrac{b}{2} & c & \dfrac{e}{2} \\ \dfrac{d}{2} & \dfrac{e}{2} & f \end{bmatrix} \end{align} \]
注意:平面上二次曲线的一般位置可由 5 点唯一确定
退化二次曲线:若矩阵 \(C\) 不是满秩的,则该曲线为退化二次曲线;若 \(\text{rk}(C) = 2\) 退化为两条直线,\(\text{rk}(C) = 1\) 则退化为一条重线
二次曲线的切线:(齐次坐标表示下)与二次曲线 \(C\) 相切于点 \(x\) 的直线 \(I\) 由 \(I = Cx\) 确定 \[ \begin{align} \text{证明:}&\text{由相切于点 }x \text{ 可知,}x^TI = x^TCx = 0 \text{ ,故 }I = Cx \text{ 过点 }x \\ &\text{假设 }I \text{ 与 } C \text{相较于另一点 }y \text{ ,则有 }x^TCx = x^TI = y^TCy = 0 \\ &\text{故 }(x + \alpha y)^T C(x + \alpha y) = 0 \text{ ,可知连接} x,y \text{的直线上所有点都在曲线 }C\text{ 上,故 }C \text{ 是退化的,证毕。} \end{align} \]
对偶二次曲线:设二次曲线为 \(C_{3 \times 3}\),则 \(C\) 的伴随矩阵 \(C^{*}\) 表示一个对偶曲线,由 \(C\) 的切线定义
- 伴随矩阵:
- 余因子矩阵:\(C^{*}_{ij} = (-1)^{ij} |\hat{C}_{ij}|\),其中 \(\hat{C}_{ij}\) 为划掉 \(C\) 的第 \(i\) 行 和 第 \(j\) 列余下的矩阵
- 伴随矩阵:余因子矩阵的转置,即 \(C^{*T}\);对于非奇异 \(C\)(需是对称的),有 \(C^{*} = C^{-1}\)
- 对于二次曲线 \(C\) 的任意切线 \(I\),均满足 \(I^T C^{*} I = 0\)
- 伴随矩阵:
射影映射的定义:是一个 \(\text{IP}^2\) 到自身的可逆映射 \(h\):三点 \(x_1, x_2, x_3\) 共线 \(\Leftrightarrow\) \(h(x_1), h(x_2), h(x_3)\) 也共线
射影映射的充要条件:映射 \(h: \text{IP}^2 \rightarrow \text{IP}^2\) 是射影映射 \(\Leftrightarrow\) 存在一个 \(3 \times 3\) 的 非奇异阵 \(H\),使对 \(\forall x \in \text{IP}^2, h(x) = Hx\)
由充要条件导出的射影变换定义:一个平面(保线)变换是关于 3 维齐次向量的一种线性变换,\(x' = Hx\),其中 \(H\) 为非奇异阵 \[ \begin{bmatrix} x_1' \\ x_2' \\ x_3 ' \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \]
注意:该变换矩阵是一个齐次矩阵,由 8 个比率决定其意义,故 9 个元素中只有 8 个自由度
直线与二次曲线的变换:
- 直线的变换:在点变换 \(x' = Hx\) 下,直线变换 \(I\) 为 \(I' = H^{-T}I\)
- 二次曲线的变换:在点变换 \(x' = Hx\) 下,二次曲线 \(C\) 变换为 \(C' = H^{-T}CH^{-1}\)
- 对偶二次曲线的变换:在点变换 \(x' = Hx\) 下,对偶二次曲线 \(C^{*}\) 变换为 \(C^{*}{'} = HC^*H^T\)
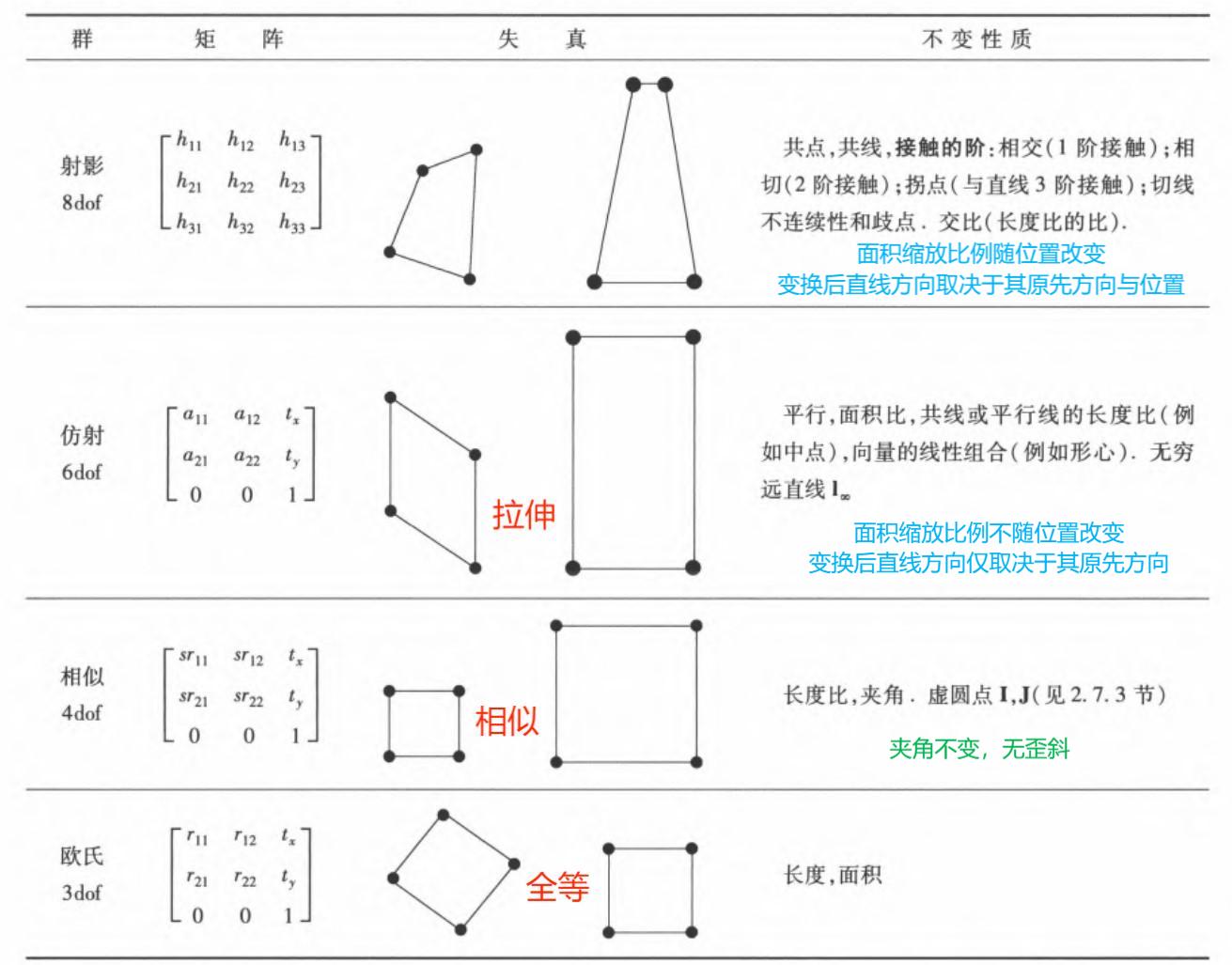
不同层次的变换:等距变换 \(\Rightarrow\) 相似变换 \(\Rightarrow\) 仿射变换 \(\Rightarrow\) 射影变换,逐步失真
等距变换:平面 \(\text{IR}^2\) 上的变换,保持欧式距离不变,3dof,可表示为: \[ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} \epsilon \cos \theta & -\sin \theta & t_x \\ \epsilon \sin \theta & \cos \theta & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \] 该变换的不变量是长度、角度、面积等;\(\epsilon = 1\) 则等距变换时保向的(欧式变换 或 刚体运动),否则是反射
相似变换:等距变换 和 均匀缩放 的复合,4dof(新增缩放自由度),在不考虑反射变换的条件下可表示为: \[ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} s \cos \theta & -s\sin \theta & t_x \\ s \sin \theta & s\cos \theta & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \] 该变换的不变量是角度、长度间比率、面积间比率;\(s\) 是缩放系数,在保持形状不变的条件下改变图形大小
仿射变换:非奇异线性变换 与 平移变换 的复合,6dof(新增拉伸方向\(\phi\) + 拉伸比例\(\lambda\)两个自由度): \[ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & t_x \\ a_{21} & a_{22} & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \] 其中 \(A\) 是一个 \(2 \times 2\) 的非奇异矩阵,可拆解为: \[ A = R(\theta)R(-\phi)\begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}R(\phi) \] 即 旋转 \(\phi\) \(\rightarrow\) 在 x 和 y 方向上分别按比例 \(\lambda_1\) 和 \(\lambda_2\) 缩放 \(\rightarrow\) 回旋 \(\phi\) \(\xrightarrow{拉伸完毕后}\) 旋转 \(\theta\)
该变换的不变量是平行线关系、平行线段长度比、面积比等;\(\det{A} = \lambda_1\lambda_2\),\(\det{A} > 0\) 说明是保向的射影变换:非齐次 非奇异线性变换 与 平移变换 的复合,8dof,可表示为: \[ x' = H_px = \begin{bmatrix} A & t \\ v^T & u \end{bmatrix}x \]
注意:射影变换 和 仿射变换 的根本区别在于 射影变换的向量 \(v \ne 0\),可将理想点变换为非理想点
射影变换的分解:一个一般的射影变换 \(H\) 可以分解为如下形式 \[ \begin{align} H &= H_SH_AH_P \\&= \begin{bmatrix} sR & t \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} K & 0\\ 0^T& 1\end{bmatrix} \begin{bmatrix} I & 0 \\ v^T & u \end{bmatrix} \\ &= \begin{bmatrix} A & vt \\ v^T & u \end{bmatrix} \end{align} \] 其中 \(A = sRK + tv^T\) 为非奇异矩阵;\(u \ne 0\) 且 当\(s > 0\)时分解是唯一的(保向)
- \(H_P\) 为 射影变换,\(I\) 是单位矩阵;该变换的dof=2,负责移动无穷远直线
- \(H_A\) 为 仿射变换,\(K\) 是满足 \(|K| = 1\) 的归一化上三角矩阵;该变换的dof=2,进一步影响仿射性质,不移动 \(I_{\infty}\)
- \(H_S\) 为 一般的相似变换,\(R\) 是旋转矩阵;该变换的dof=4,不影响仿射和射影性质
注意:由于 \(H_P^{-1}\)、\(H_A^{-1}\)、\(H_{S}^{-1}\) 仍分别是 射影变换、仿射变换和相似变换,故 \(H^{-1} = H_P^{-1}H_A^{-1}H_{S}^{-1}\) 同样仍是射影变换
由图像恢复仿射和度量性质:
无穷远直线:在射影变换 \(H\) 下,无穷远直线 \(I_{\infty}\) 仍为无穷远直线 \(\Leftrightarrow\) \(H\) 是仿射变换,证明如下 \[ \begin{align} &\text{必要性:设 }H\text{ 是仿射变换:}I'_{\infty} = H_A^{-T} I_{\infty} = \begin{bmatrix} A^{-T} & 0 \\ -t^TA^{-T} & 1 \\ \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = I_{\infty} \\ &\text{充分性:若要让无穷远点被映射为一个无穷远点,由于 } \begin{bmatrix} A & t \\ v^T & u \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ 0 \end{bmatrix} = \begin{bmatrix} A\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \\ v_1x_1 + v_2x_2 \end{bmatrix} \\ & \text{只需令 } v_{1} = v_{2} = 0\text{ ,即该变换是仿射变换,证毕。} \end{align} \]
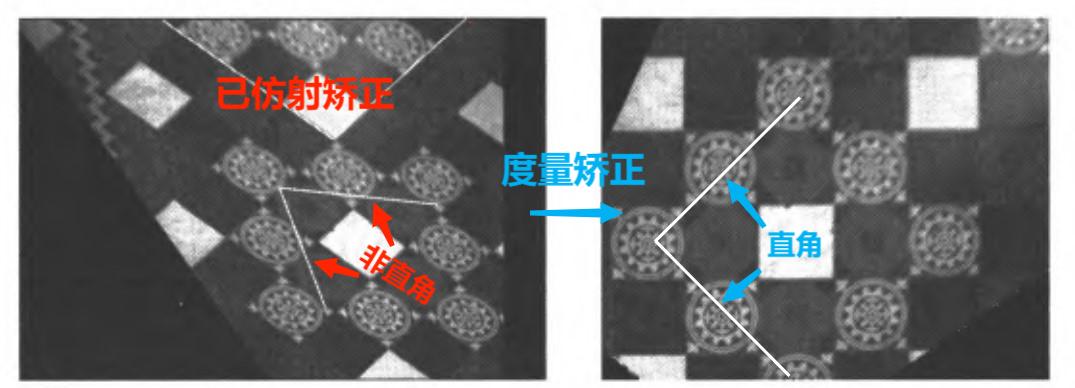
恢复仿射性质:关键在于辨认出透视图象上的 无穷远直线
核心思想:世界图像中两直线 相交于 \(I_{\infty}\) 在 \(\text{IP}^2\) 的像上 \(\Rightarrow\) 世界图像中的两直线平行
- 欧式平面中的平行线相交于 \(I_{\infty}\) \(\Rightarrow\) 射影空间中的平行线相交于 \(I\)
- 射影变换保持交点不变 \(\Rightarrow\) 经过射影变换后的两条直线仍相交于 \(I_{\infty}\) 经射影变换的像 \(I\) 上
注意:\(I_{\infty}\) 在真实世界内是看不见的,但其转换到 \(\text{IP}^2\) 中是可视的直线 \(I\)
仿射矫正:设 无穷远直线 的像是 \(I = (l_1, l_2, l_3)^T\)(\(l_3 \ne 0\)),则把 \(I\) 映射回不可见的 \(I_{\infty} = (0, 0, 1)^T\) 的合适的射影变换如下: \[ \begin{align} H = H_A \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ l_1 & l_2 & l_3 \end{bmatrix} \end{align} \] 其中 \(H_A\) 可以为任何的仿射变换;且总有 \(H^{-T}(l_1, l_2, l_3)^T = (0, 0, 1)^T = I_{\infty}\),即把无穷远直线的像映射回 \(I_{\infty}\)
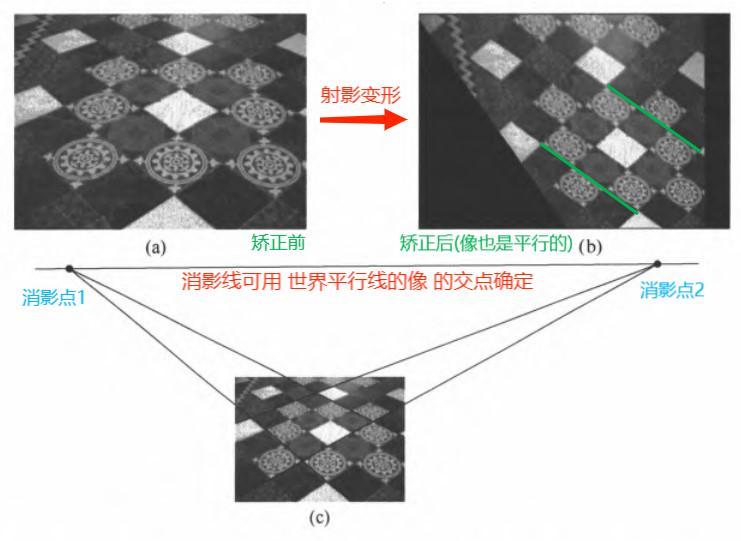
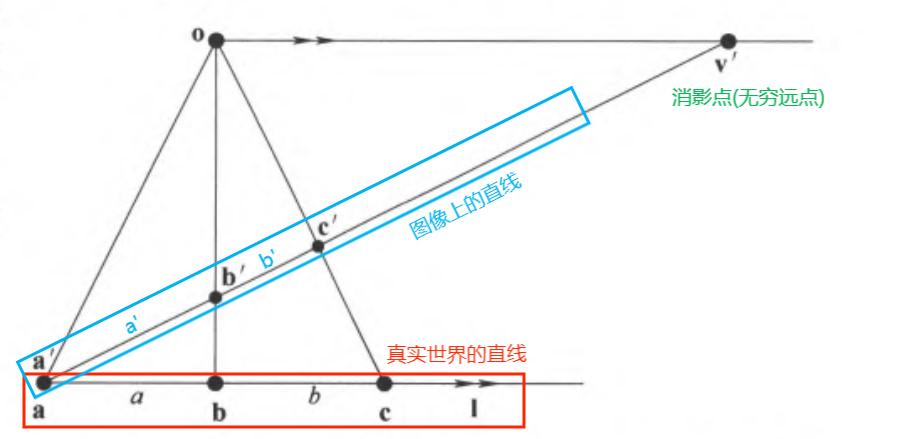
消影点:世界平行线的交点在 \(\text{IP}^2\) 中的像,也就是欧氏空间中的无穷远点
利用长度比例计算消影点:设世界直线上的共线三点为 \(a, b, c\),图像上对应的共线三点为 \(a', b', c'\)
- 确定现实世界中的距离比:\(d(a, b):d(b,c) = a:b\),设世界齐次坐标为 \((0,1)^T, (a,1)^T,(a+b, 1)^T\)
- 在图像上量出距离比:设 \(d(a', b') : d(b',c') = a':b'\),设图像齐次坐标为 \((0, 1)^T, (a', 1)^T, (a'+b', 1)^T\)
- 计算使 \(a \rightarrow a'\),\(b \rightarrow b'\),\(c \rightarrow c'\) 的 1D 射影变换 \(H_{2 \times 2}\)
- 直线 \(a'b'c'\) 的消影点是变换 \(H_{2 \times 2}\) 下无穷远点 \((1, 0)^T\) 的像
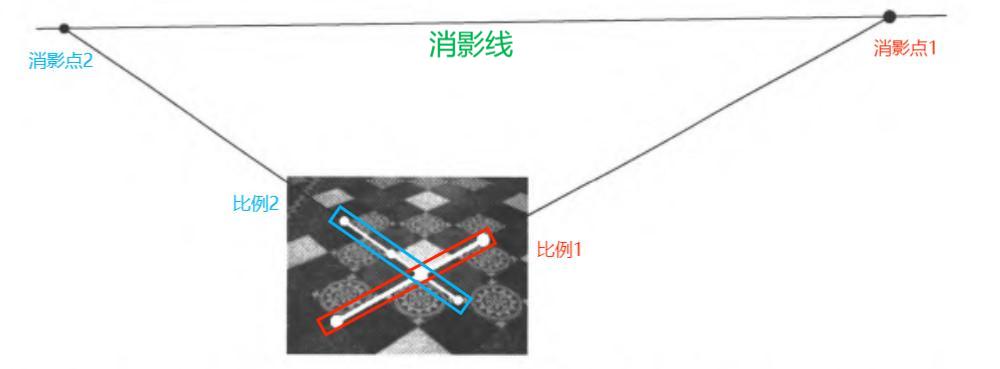
由长度比确定消影点的几何作图法:具体如下图所示
- 确定现实世界中的距离比:\(d(a, b):d(b,c) = a:b\)
- 在图像上量出距离比:\(d(a', b') : d(b',c') = a':b'\)
- 过图上 \(a'\) 画任意直线 \(l\),令直线上 \(a = a'\)、\(||ab|| : ||bc|| = a : b\)
- 连接 \(bb'\) 和 \(cc'\) 并交于图上点 \(o\);过 \(o\) 作平行于 \(l\) 的直线,交 \(a'c'\) 于消影点 \(v'\)
已知图上两个消影点 \(\Rightarrow\) 连接该两点得到图上消影线
虚圆点及其对偶:
虚圆点:在任何相似变换下,\(I = (1, i, 0)^T\) 和 \(J = (1, -i, 0)^T\) 是 \(I_{\infty}\) 的两个不动点(共轭理想点),即: \[ \begin{align} I' &= H_s I \\ & = \begin{bmatrix} s\cos \theta & -s \sin \theta & t_s \\ s \sin \theta & s \cos \theta & t_y \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 \\ i \\ 0 \end{bmatrix} = se^{-i\theta} \begin{bmatrix} 1 \\ i \\ 0 \end{bmatrix} = I \end{align} \]
注意:在射影变换 \(H\) 下,虚圆点 \(I\) 和 \(J\) 为不动点 \(\Leftrightarrow\) \(H\) 为相似变换
虚圆点的意义:任意平面圆周与 \(I_{\infty}\) 相交于 虚圆点,证明如下: \[ \begin{align} &\text{当二次曲线为圆时有:}x_1^2 + x_2^2 + dx_1x_2 + ex_2x_3 + fx_3^2 = 0 \\ &\text{令该二次曲线与 }I_{\infty} 相交于 \textbf{理想点,即 }x_3 = 0 \text{ ,则 } x_1^2 + x_2^2 = 0 \\ &\text{解得 }I = (1, i, 0)^T \text{,}J = (1, -i, 0)^T \text{ ,证毕。} \end{align} \]
虚圆点的对偶:二次曲线 \(C_{\infty}^{*} = IJ^T + JI^T\) 与 虚圆点 对偶;\(C_{\infty}^{*}\) 表示两个虚圆点构成的退化二次曲线(\(\text{rk} = 2\)),在欧式坐标系下具体表示为: \[ \begin{align} C_{\infty}^* &= \begin{bmatrix} 1 \\ i \\ 0 \end{bmatrix} \begin{bmatrix} 1 & -i & 0 \end{bmatrix} + \begin{bmatrix} 1 \\ -i \\ 0 \end{bmatrix} \begin{bmatrix} 1 & i & 0 \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0\end{bmatrix} \end{align} \] \(I_{\infty}\) 是 \(C_{\infty}^*\) 的零向量:\(C_{\infty}^* I_{\infty} = I(J^TI_{\infty}) + J(I^TI_{\infty}) = 0\)
(虚圆点在 \(I_{\infty}\) 上,故总有 \(I^TI_{\infty} = J^T I_{\infty} = 0\))\(C_{\infty}^{*}\) 在射影变换 \(H\) 下不变 \(\Leftrightarrow\) \(H\) 是相似变换
射影平面上的夹角:
- 欧氏几何两直线夹角:\(\cos \theta = \dfrac{l_1m_1 + l_2 m_2}{\sqrt{(l_1^2 + l_2^2) (m_1^2 + m_2^2)}}\),其中直线 \(l = (l_1, l_2, l_3)^T\),直线 \(m = (m_1, m_2, m_3)^T\)
- 射影几何两直线夹角:\(\cos \theta = \dfrac{l^T C_{\infty}^*m}{\sqrt{(l^TC_\infty^*l)(m^TC_{\infty}^*m)}}\),该公式在射影变换前后保持不变
- \(l^T C_{\infty}^{*}m = 0\) \(\Rightarrow\) 直线 \(l\) 和 \(m\) 垂直
恢复度量性质:关键在于辨认出射影平面上的 \(C_{\infty}^{*}\);设点变换为 \(x' = Hx\),由 \(H\) 的链式分解: \[ \begin{align} C_{\infty}^{*}{'} &= (H_PH_AH_S)C_{\infty}^{*} (H_PH_AH_S)^T \\ &= \begin{bmatrix} KK^T & K^Kv \\ v^TKK^T & v^TKK^Tv \\ \end{bmatrix} \end{align} \] 根据上面的分解式可知,射影成分 \(v\) 和 仿射成分 \(K\) 可直接根据 \(C_{\infty}^{*}\) 的像确定;同时由 SVD 分解: \[ \begin{align} C_{\infty}^{*}{'} &= UC_{\infty}^{*} U^T \\ &= U\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} U^T \end{align} \] 通过将上式 与 \(H\) 的分解式做对比,可以解得 \(K\) 和 \(v\),从而求出 仅相差一个相似变换 的矫正射影变换 \(H = U\)
在已经过仿射矫正的图像上进行度量矫正:设图像中直线 \(I'\) 和 \(m'\) 与 世界平面中的一对垂直直线 \(I\) 和 \(m\) 相对应
由夹角公式推论可知,即便经过射影变换,仍有不变式 \(I' C_{\infty}^{*}{'} m'= 0\),令 \(v = 0\) 并展开为矩阵方程形式为: \[ \begin{align} &\begin{pmatrix} l_1', l_2', l_3' \end{pmatrix} \begin{bmatrix} KK^T & \textbf{0} \\ \textbf{0}^T & 0 \end{bmatrix} \begin{pmatrix} m_1' \\ m_2' \\ m_3' \end{pmatrix} = 0 \\ &\text{即 }\begin{pmatrix} l_1', l_2' \end{pmatrix} KK^T (m_1', m_2')^T = 0 \end{align} \]
\(KK^T\) 是实对称正定阵;由上式求出 \(KK^T\) 后,进一步利用分解算法(如 Cholesky 分解法)求出 \(K\)
注意:由于仍相差一步 相似变换,故矫正后的图像和真实图像间存在缩放差距
二、3D 射影几何
三维空间中的点:用四维度齐次向量 \(\textbf{X} = (X_1, X_2, X_3, X_4)\) 表示;欧氏空间 和 射影空间 之间的转换 与 2D 类似:
- \(\text{IP}^4 \Rightarrow \text{IR}^3\):设 三维欧氏空间中的点坐标为 \((X, Y, Z)\),则有 \(X = \dfrac{X_1}{X_4}\),\(Y = \dfrac{X_2}{X_4}\),\(Z = \dfrac{X_3}{X_4}\)
- \(\text{IR}^3 \Rightarrow \text{IP}^4\):直接追加一个"1",即 \(\textbf{X} = (X, Y, Z, 1)\)
\(\text{IP}^3\) 上的射影变换:点线性变换 \(X' = HX\),其中 \(H_{4 \times 4}\) 为非奇异阵,共有 16 - 1 = 15 dof,
三维空间中的平面:
齐次 与 非齐次 表示:
非齐次表示:3D 空间中的平面可表示为 \(\pi_1 X + \pi_2 Y + \pi_3 Z + \pi_4 = 0\)
- 法线方程:\(n = (\pi_1, \pi_2, \pi_3)^T\)
- 非齐次向量:\(\widetilde{X} = (X, Y, Z)\) \(\Rightarrow\) 非齐次平面方程 \(n \widetilde{X} + d = 0\)
- 原点到平面距离 \(= \dfrac{d}{||n||}\),其中 \(d = \pi_4\)
齐次表示:用代换 \(X = \dfrac{X_1}{X_4}\),\(Y = \dfrac{X_2}{X_4}\),\(Z = \dfrac{X_3}{X_4}\),对应的齐次形式为 \(\pi_1 X_1 + \pi_2 X_2 + \pi_3 X_3 + \pi_4 X_4 = 0\)
或有简洁形式 \(\pi^T X = 0\),即用在平面 \(\pi\) 上的点 \(X\) 表示平面,\(\pi = (\pi_1, \pi_2, \pi_3, \pi_4)^T\) 是平面的齐次表示
3D点与平面的关系:
平面可以由一般位置的三个点确定:设三个点 \(X_i\) 都在平面 \(\pi\) 上,则有 \(\pi^T X_i = 0\)(\(i = 1, 2, 3\)),则有: \[ \begin{align} \begin{bmatrix} X_1^T \\ X_2^T \\ X_3^T \end{bmatrix}\pi = 0 \end{align} \]
注意:若 \(X_i\) 三点线性无关,则三个点组成的 \(3 \times 4\) 的矩阵秩为3;若这些点共线,则矩阵的秩为2,定义了以共线点组成直线为轴的平面束
三个一般的平面确定一点:设三个平面 \(\pi_i\) 相交于点\(X\),则 \(X\) 可由下面的矩阵方程求解: \[ \begin{align} \begin{bmatrix} \pi_1^T \\ \pi_2^T \\ \pi_3^T \end{bmatrix}X = 0 \end{align} \]
射影变换:在点变换 \(X' = H^{-T}X\) 下,平面变换为 \(\pi' = H\pi\)
三维空间中的直线:
连线表示:设 \(A\) 和 \(B\) 是两个不重合的空间点,则连接两点的直线可由 \(W_{2\times4}\) 表示: \[ \begin{align} &W = \begin{bmatrix} A^T \\ B^T \end{bmatrix} \\ &\text{例如:}X轴可表示为\text{ } W =\begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ \end{bmatrix} \\ &\text{即原点 和 X方向无穷远点的连线} \end{align} \]
- \(W^T\) 的生成子空间是在直线 \(\lambda A + \mu B\) 上的点集,即 \(W^T\) 列向量张成的子空间
- \(W\) 的零子空间是以该直线为轴的平面束,即令 \(Wx = 0\) 的平面 \(x_{4\times1}\) 的集合
连线的对偶表示:设 \(P\) 和 \(Q\) 是两个一般的平面,则两平面的交线可由 \(W^{*}_{2\times4}\) 表示 \[ \begin{align} &W^* = \begin{bmatrix} P^T \\ Q^T \end{bmatrix} \\ &\text{例如:}X轴可表示为 \text{ } W^{*}= \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \\ &\text{即 } XY \text{ 和 }XZ\text{ 平面}的交线 \end{align} \]
- \(W^{*T}\) 的生成子空间是以该直线为轴的平面束 \(\lambda P + \mu Q\),即 \(W^{*T}\) 列向量张成的子空间
- \(W^{*}\) 的零子空间是该交线上的点集,即令 \(Wx = 0\) 的点 \(x_{4\times1}\) 的集合
\(\text{Pl}\ddot{\text{u}}\text{cker}\) 矩阵表示:设两点为 \(A\) 和 \(B\),则连接两点的直线可表示为反对称齐次矩阵 \(L_{4 \times 4} = AB^T - BA^T\)
- 矩阵 \(L\) 的元素表示为 \(l_{ij} = A_iB_j - B_iA_j\)
- \(\text{rk(L)} = 2\),其 2 维零空间由以该直线为轴的平面束组成,即令 \(Lx = 0\) 的平面 \(x_{4\times1}\) 组成
- \(L = AB^T - BA^T\) 是平面关系 \(I = x \times y\) 的高维度推广(\(x, y\) 是 3D 向量)
- 在点变换 \(X' = HX\) 下,矩阵变换为 \(L' = HLH^T\)
注意:矩阵 \(L\) 与定义其的 \(A\) 和 \(B\) 无关:令直线 \(AB\) 上一点 \(C = A + \mu B\) 代替 \(B\),新定义下仍有 \(L' = L\)
\(\text{Pl}\ddot{\text{u}}\text{cker}\) 矩阵对偶表示:设 \(P\) 和 \(Q\) 是两个一般的平面,则两平面的交线可表示为对偶 \(L^{*} = PQ^T - QP^T\)
- 快速重写 \(L^{*}\) 中的非零元素:\(l_{34}^{*}:l_{42}^{*}:l_{23}^{*}:l_{14}^{*}:l_{13}^{*}:l_{12}^{*}\) = \(l_{12}:l_{13}:l_{14}:l_{23}:l_{42}:l_{34}\)
- 在点变换 \(X' = HX\) 下,矩阵变换为 \(L^{*}{'} = H^{-T}L^{*}H^{-1}\)
- 由 点\(X\) 和 直线\(L\) 联合确定的平面 \(\pi = L^{*}X\);且 \(L^{*} X = 0\) \(\Leftrightarrow\) 点\(X\) 在 直线\(L\) 上
- 由 点\(X\) 和 平面\(\pi\) 联合确定的点 \(X = L \pi\);且 \(L \pi = 0\) \(\Leftrightarrow\) 直线\(L\) 在 平面\(\pi\)上
\(\text{Pl}\ddot{\text{u}}\text{cker}\) 直线坐标:Plucker矩阵\(L\) 的 6 个非零元素,即 \(\mathcal{L} = \{l_{12}, l_{13}, l_{14}, l_{23}, l_{42}, l_{34}\}\)
- 唯有满足 \(l_{12}l_{34} + l_{13}l_{42} + l_{14}l_{23} = 0\),\(\mathcal{L}\) 才对应于一条 3D 直线;该约束称为 Klein二次约束
- 设直线 \(\mathcal{L}\) 和 \(\hat{\mathcal{L}}\) 分别由连接 \(AB\) 和 连接 \(\hat{A}\hat{B}\) 获得,则 \(\mathcal{L}\) 和 \(\hat{\mathcal{L}}\) 相交(共面) \(\Leftrightarrow\) \(\det{[A, B, \hat{A}, \hat{B}]} =
(\mathcal{L}|\hat{\mathcal{L}}|) = 0\)
其中 \((\mathcal{L}|\hat{\mathcal{L}}|)\) 是双线性乘积,可证明 \((\mathcal{L}|\hat{\mathcal{L}}|) = l_{12}\hat{l}_{34} + \hat{l}_{12}l_{34} + l_{13}\hat{l}_{42} + \hat{l}_{13}l_{42} + l_{14}\hat{l}_{23} + \hat{l}_{14}l_{23}\)- 若 \((\mathcal{L}|\hat{\mathcal{L}}|) = 0\),则 6 维向量 \(\mathcal{L}\) 仅表示 \(\text{IP}^3\) 中的一条直线,与 Klein约束等价
- 若两直线 \(\mathcal{L},
\hat{\mathcal{L}}\) 分别是平面 \(P,
Q\) 和 \(\hat{P}, \hat{Q}\)
的交线,那么 \((\mathcal{L |
\hat{\mathcal{L}}|}) = \det{[P, Q, \hat{P}, \hat{Q}]}\)
且同样有 \((\mathcal{L} | \hat{\mathcal{L}}) = 0\) \(\Leftrightarrow\) 两条平面交线相交 - 若 \(\mathcal{L}\) 是两平面 \(P, Q\) 的交线,\(\hat{\mathcal{L}}\) 是两点 \(A, B\) 的连线,则 \((\mathcal{L}|\hat{\mathcal{L}}|) = (P^TA)(Q^TB) - (Q^TA)(P^TB)\)
三、2D 变换估计
直接线性变换(DLT)算法:由 \(n \ge 4\) 组 2D 到 2D 的点对 \(\textbf{x}_i \leftrightarrow \textbf{x}_i'\) 确定变换 \(\textbf{H}\) 的一种简单线性算法
若把矩阵 \(\textbf{H}\) 的第 \(j\) 行记作 \(h^{jT}\),则有: \[ \begin{align} &\textbf{H}\textbf{x}_i = \begin{bmatrix} h^{1T}\textbf{x}_i \\ h^{2T}\textbf{x}_i \\ h^{3T}\textbf{x}_i \end{bmatrix} \\ &\text{其中 }h^{jT} \text{ 表示矩阵 }\textbf{H}\text{ 的第}j\text{行} \end{align} \] 记齐次向量 \(\textbf{x}_i' = (x_i', y_i', \omega_i')^T\);由于变换前 \(\textbf{x}_i\) 和 变换后 \(\textbf{x}_i' = \textbf{H}\textbf{x}_i\) 有相同的方向,故 \(\textbf{x}_i'\times \textbf{H}\textbf{x}_i = 0\),即: \[ \begin{align} &\textbf{x}_i'\times \textbf{H}\textbf{x}_i = \begin{bmatrix} y_i'h^{3T}\textbf{x}_i - \omega_i' h^{2T}\textbf{x}_i \\ \omega_i'h^{1T}\textbf{x}_i - {x}_i'h^{3T}\textbf{x}_i \\ x_i'h^{2T} \textbf{x}_i - y_i'h^{1T}\textbf{x}_i \end{bmatrix} = 0 \\ \\ &\text{由于 } h^{jT}\textbf{x}_i = \textbf{x}_i^Th^j \text{ ,故上式可改写为矩阵方程:} \\ &\text{A}_ih = \begin{bmatrix} 0^T & -\omega_i'\textbf{x}_i^T & y_i'\textbf{x}_i^T \\ \omega_i'\textbf{x}_i^T & 0^T & -x_i'\textbf{x}_i^T \\ -y_i'\textbf{x}_i^T & x_i'\textbf{x}_i^T & 0^T \end{bmatrix} \begin{bmatrix} h^1 \\ h^2 \\ h^3 \end{bmatrix} = 0 \end{align} \]
对于每个点 \(\textbf{x}_i\) 都有 \(\text{A}_ih = 0\) 的形式,其中 \(\text{A}_i\) 形状为 \(3 \times 9\),\(h\) 形状为 \(9 \times 1\)
- 由于 \(\text{A}_i\) 的第三行可由第一二行线性表出,故在解 \(\textbf{H}\) 时可将第三行忽略,即 \(\text{A}_i\) 形状为 \(2 \times 9\)
- 解 \(H\) 时可取 \(\omega_i = 1\),此时 \((x_i', y_i')^T\) 是图像中测量得到的坐标
把 \(n\) 个 \(2\times 9\) 的矩阵 \(\text{A}_i\) 合并成一个 \(2n \times 9\) 的大矩阵 \(\text{A}\)
注意:之所以要用 \(n \ge 4\) 个点对,是因为 \(h\) 有 9 个元素,抛开缩放因子有 8 个自由度,故需要至少 4 个点对解出 \(\text{H}\)
求解 \(\text{A}\) 的 SVD,对应于最小奇异值的单位奇异向量就是解\(h\): \[ \begin{align} &\text{若 } \textbf{H} = \begin{bmatrix} h_1 & h_2 & h_3 \\ h_4 & h_5 & h_6 \\ h_7 & h_8 & h_9 \\ \end{bmatrix} \\ &\text{则 }h_i\text{ 是解 }h\text{ 的第} i\text{个元素;求出 }h\text{ 即是求出 }\textbf{H} \end{align} \] 为什么要求最小特征值的单位向量?
图像上坐标的测量通常是不准确的(又称噪声),这导致方程 \(\text{A}h = 0\) 不存在精确解,只能找近似解
因此可考虑最小化范数 \(||\text{A}h||\);为避免出现平凡解 \(h = 0\),可在最小化过程中添加一个约束 \(||h || = 1\)
以上表述等价于求商 \(\dfrac{||\text{A}h||}{||h||}\) 的最小值问题,该问题的解法如下: \[ \begin{align} &\text{目标:给定一个行数不少于列数的矩阵} \text{A}\text{,最小化} ||\text{A}h||\text{ 满足 }||h|| = 1\text{ 的解 } x \\ &\text{算法:求解 }\text{A}\text{ 的 }\textbf{SVD}\text{ ,即 }\text{A} = \textbf{UDV}^T\text{,解出 }h\text{ 是 }\textbf{V}\text{ 的最后一列} \\ &\qquad \text{ }\text{ 同时也是 }\text{A}^T\text{A}\text{ 的}\textbf{最小特征值}\text{对应的单位特征向量} \end{align} \]注意:对于求解超定解问题(方程数 > 未知数数),一般通过优化方法找到近似解
不同的代价函数:
代数距离:累积计算各点对 \(\textbf{x}_i \leftrightarrow \textbf{x}_i'\) 对应的误差向量 \(\epsilon_i\),单个误差向量可表示为: \[ \begin{align} d_{alg}(\textbf{x}_i', \textbf{H}\textbf{x}_i)^2 &= ||\epsilon_i||^2 \\ &= ||\begin{bmatrix} 0^T & -\omega_i'\textbf{x}_i^T & y_i'\textbf{x}_i^T \\ \omega_i' \textbf{x}_i^T & 0^T & -x_i'\textbf{x}_i^T \end{bmatrix}||^2 \\ \end{align} \] 在 DLT 算法中,给定点对集合,\(\epsilon = \text{A}h\) 是整个代数误差向量,即 \(\sum_{i}||\epsilon_i|| = ||\text{A}h||^2 = ||\epsilon||^2\)
几何距离:最小化 图像坐标测量值 和 估计值 差距
记号:\(\textbf{x}\) 表示测量点的图像坐标,\(\hat{\textbf{x}}\) 表示点的估计值,\(\overline{\textbf{x}}\) 表示点的真值
单幅图像误差:假设第一幅图\(\textbf{x}\)非常精确(经过标定),误差仅出现在第二幅图测量点\(\textbf{x}'\),欧氏距离记作 \(d(\textbf{x}, \textbf{y})\) \[ \begin{align} &\text{转移误差}=\sum_{i}d(\textbf{x}_i', \textbf{H}\overline{\textbf{x}}_i)^2 \\ &\text{算法要估计使上式误差值最小的单应 }\hat{\textbf{H}} \end{align} \]
对称图像误差:一般情况下两幅图都有测量误差,需同时考虑双向变换: \[ \begin{align} &\text{对称转移误差}=\sum_{i}d(\textbf{x}_i, \textbf{H}^{-1}\textbf{x}_i')^2 + d(\textbf{x}_i', \textbf{H}\textbf{x}_i)^2 \\ &\text{算法要估计使上式误差值最小的单应 }\hat{\textbf{H}} \end{align} \] 第一项是第一幅图像的后向转移误差,第二项是第二幅图的前向转移误差
重投影误差:评估每组点对应的"校正值",即实际测量值 和 所求估计值之间的误差 \[ \begin{align} &\sum_{i}d(\textbf{x}_i, \hat{\textbf{x}}_i)^2 + d(\textbf{x}_i', \hat{\textbf{x}}_i')^2 \\ & \text{s.t. }\hat{\textbf{x}_i'} = \hat{\textbf{H}}\hat{\textbf{x}}_i \text{ }(\forall i) \\ \end{align} \] 最小化上式需要同时确定 \(\hat{\textbf{H}}\) 以及附加的完全匹配的点对 \(\hat{\textbf{x}}_i \leftrightarrow \hat{\textbf{x}}'_i\);其中 \(\hat{\textbf{H}}\) 是用某种算法求解的初始校正映射
注意:\(\textbf{x}'\) 和 \(\textbf{H}\textbf{x}\) 不完全对应(存在误差),但估计的点 \(\hat{\textbf{x}}\) 和 \(\hat{\textbf{x}}'\) 却通过 \(\hat{\textbf{x}}' = \textbf{H}\hat{x}\) 完全对应
Sampson误差:重投影误差优化的参数 \(\textbf{H}\) 初值可由 DLT 算法近似给出,但 \(\hat{\textbf{x}}\) 和 \(\hat{\textbf{x}}'\) 仍"悬而未定"
将测量点对 \(\textbf{x}\) 和 \(\textbf{x}'\) 的非齐次坐标拼起来作为 \(\text{IR}^4\) 的一个点 \(\textbf{X} = (x_i, y_i, x_i', y_i')^T\)
注意:由于矩阵方程 \(\text{A}_i h = 0\) 中 \(\text{A}_i\) 的每一行都是关于 \(x_i, y_i, x_i', y_i'\) 的二次方程,故 \(\textbf{X} \in \mathcal{V}_2\)
令 \(\hat{\textbf{X}}_i = (\hat{x}_i, \hat{y}_i,\hat{x}_i',\hat{y}_i')^T\),\(||\textbf{X}_i - \hat{\textbf{X}}_i|| = (x_i - \hat{x}_i)^2 + \cdots (y_i' - \hat{y}_i')\) = 重投影误差
故优化重投影误差 \(\Leftrightarrow\) 找到 \(\mathcal{V}_2\) 上最靠近 \(\textbf{X}_i\) 的点 \(\hat{\textbf{X}}_i\);由于 \(\mathcal{V}_2\) 是非线性的,故可考虑估计 \(\hat{\textbf{X}}\) 的一阶近似对于给定单应 \(\textbf{H}\),将误差函数记作有关 \(\textbf{X}\) 的 2 维向量 \(\mathcal{C}_\textbf{H}(\textbf{X})\),用 Taylor 展开对其一阶逼近: \[ \begin{align} \mathcal{C}_{\textbf{H}}(\textbf{X} + \delta_\textbf{X}) = \mathcal{C}_\textbf{H}(\textbf{X}) + \dfrac{\partial \mathcal{C}_\textbf{H}}{\partial \textbf{X}} \delta_\textbf{X} \end{align} \] 记 \(\delta_{\textbf{X}} = \hat{\textbf{X}} - \textbf{X}\),当 \(\hat{\textbf{X}} \in \mathcal{V}_2\) 时有 \(\mathcal{C}_\textbf{H}(\hat{\textbf{X}}) = 0\),即 \(\mathcal{C}_\textbf{H}(\textbf{X} + \delta_\textbf{X}) = 0\)
故上式可化为 \(\textbf{J} \delta_{\textbf{X}} + \epsilon= 0\),其中 \(\textbf{J} = \dfrac{\partial \mathcal{C}_\textbf{H}}{\partial \textbf{X}}\) 为偏导数矩阵,\(\epsilon = \mathcal{C}_\textbf{H}(\textbf{X}) = A_ih\) 为关于 \(\textbf{X}\) 的代价函数要求解 \(\hat{\textbf{X}}\),只要求解满足 \(\textbf{J}\delta_\textbf{X} = -\epsilon\) 的约束下使 \(||\delta_\textbf{X}||\) 取最小值的向量 \(\delta_\textbf{X}\)(可使用 Lagrange 乘子法)
解得 \(\delta_\textbf{X} = -\textbf{J}^T (\textbf{J}\textbf{J}^T)^{-1}\epsilon\),\(\hat{\textbf{X}} = \textbf{X} + \delta_\textbf{X}\),其中范数 \(||\delta_\textbf{X}||^2 = \delta_\textbf{X}^T\delta_\textbf{X}\) 即是 Sampson误差
统计代价函数:设每张图像测量坐标都有零均值和均匀标准方差的高斯噪声,则每个独立测量点\(\textbf{x}\)的PDF为: \[ \begin{align} \text{Pr}(\textbf{x}) = (\dfrac{1}{2\pi \sigma^2})e^{-\dfrac{d(\textbf{x}, \overline{\textbf{x}})^2}{2\sigma^2}} \end{align} \]
单图像误差:假设误差仅出现于第二幅图象,则获得点对集 \(\{\overline{\textbf{x}}_i \leftrightarrow \textbf{x}_i'\}\) 的概率是单个 PDF 的乘积: \[ \begin{align} &\text{Pr}(\{\textbf{x}_i'\} | \textbf{H}) = \prod_{i} (\frac{1}{2\pi \sigma^2})e^{-\dfrac{d(\textbf{x}_i', \textbf{H}\overline{\textbf{x}}_i)^2}{2\sigma^2}} \end{align} \] 其中符号 \(\text{Pr}(\{\textbf{x}_i'\} | \textbf{H})\) 表示给定真实单应 \(\textbf{H}\) 时获得测量 \(\{\textbf{x}_i'\}\) 的概率分布,其对数似然为: \[ \begin{align} \log{\text{Pr}(\textbf{x}_i' | \textbf{H})} = -\dfrac{1}{2\sigma^2}\sum_{i} d(\textbf{x}_i', \textbf{H}\overline{\textbf{x}}_i)^2 + \text{const} \end{align} \] 故对数最大似然估计 \(\Leftrightarrow\) 最小化 \(\sum_{i}d(\textbf{x}_i', \textbf{H}\overline{\textbf{x}}_i)^2\),也就等价于最小化几何误差
双图像误差:设真值点对集为 \(\{\overline{\textbf{x}}_i \leftrightarrow \overline{\textbf{x}}_i' = \textbf{H}\overline{\textbf{x}}_i \}\),则受噪声干扰的点对概率分布是: \[ \begin{align} \text{Pr}(\{\textbf{x}_i, \textbf{x}_i'\} | \textbf{H}, \{\overline{\textbf{x}}_i\}) = \prod_{i} (\dfrac{1}{2\pi \sigma^2}) e^{-\dfrac{d(\textbf{x}_i, \overline{\textbf{x}}_i')^2 + d(\textbf{x}_i', \textbf{H}\overline{\textbf{x}}_i)^2}{2\sigma^2}} \end{align} \] 用校正点对 \(\{\hat{\textbf{x}}_i \leftrightarrow \hat{\textbf{x}}_i' \}\) 替换真值点对,可得到: \[ \begin{align} \sum_{i} d(\textbf{x}_i, \hat{\textbf{x}}_i)^2 + d(\textbf{x}_i', \hat{\textbf{x}}_i')^2 \end{align} \] 目标是求解最小化上式的单应 \(\hat{\textbf{H}}\) 和 校正点对 \(\{\hat{\textbf{x}}_i \leftrightarrow \hat{\textbf{x}}_i'\}\),其中校正点对满足约束 \(\hat{\textbf{x}}' = \hat{\textbf{H}}\hat{\textbf{x}}_i\)
归一化变换:这一步预处理是很有必要的,绝对不是可有可无的
\(\{\textbf{x}_i \leftrightarrow \textbf{x}_i'\}\) 中 \((x, y, \omega)^T\) 的典型数量级为 \(100:100:1\),这导致 DLT 算法的大矩阵 \(\text{A}\) 中的元素量级差别过大:
- \(\text{A}\) 中 \(xx', xy'\) 等都是 \(10^4\)
- \(\text{A}\) 中 \(x\omega', y\omega'\) 等都是 \(10^2\)
- \(\text{A}\) 中 \(\omega\omega'\) 量级为 单位 \(1\)
归一化提高了结果的精度,需要在实施 DLT 算法前施行;归一化算法流程如下:
- 计算一个相似变换 \(\textbf{T}\),将第一幅图的点集 \(\textbf{x}_i\) 变换到新的点集 \(\tilde{\textbf{x}}_i\):
- 使点集 \(\tilde{\textbf{x}}_i\) 的形心归于图像原点 \((0, 0)^T\)
- 使点集 \(\tilde{\textbf{x}}_i\) 到图像原点的平均距离为\(\sqrt{2}\)
- 针对第二幅图的点集 \(\textbf{x}_i'\),类似上面计算一个相似变换 \(\textbf{T}'\),将 \(\textbf{x}_i'\) 变换到 \(\tilde{\textbf{x}}_i'\)
- 使用 DLT 算法计算 \(\{\tilde{\textbf{x}}_i \leftrightarrow \tilde{\textbf{x}}_i' \}\) 的单应 \(\tilde{\textbf{H}}\)
- 解除归一化:令 \(\text{H} = \text{T}'^{-1}\tilde{\textbf{H}}\text{T}\),把 \(\tilde{\textbf{H}}\) 还原回 \(\text{H}\),\(\text{H}\) 即为所求的原点对上的单应
黄金标准算法⭐:给定 \(n > 4\) 组图像点对 \(\{\textbf{x}_i \leftrightarrow \textbf{x}_i'\}\),确定两图像间的单应估计 \(\hat{\textbf{H}}\),以及使重投影误差最小的附属点集 \(\{\hat{\textbf{X}}_i\}\)
- 借助图像上四组点使用归一化的 DLT 算法计算一个初始估计 \(\hat{\textbf{H}}\)
- 选取恰当的误差函数,借助 Sampson误差式 确定附属变量 \(\{\hat{\textbf{x}}_i\}\) 的初始估计
- 在 \(\hat{\textbf{H}}\) 和 \(\hat{\textbf{x}}_i\) (\(i = 1 \dots n\)) 上最小化
重投影误差函数 \(\sum_{i}d(\textbf{x}_i, \hat{\textbf{x}}_i)^2 +
d(\textbf{x}', \hat{\textbf{x}}_i')^2\)
注意:待优化参数共有 \(2n + 9\) 个,分别是 \(2n\) 个估计点对和 9 个 \(\textbf{H}\) 的元素
四、鲁棒估计
RANSAC:对含有野值的数据集 \(S\) 进行鲁棒拟合;"野值"指测量误差之外的点(不服从正态分布),严重干扰单应的估计
核心思想:记处在模型容忍阈值 \(t\) 的样本点为模型内点,迭代选出使内点数量最多的模型
距离阈值 \(t\):设阈值 \(t\) 能使样本点为内点的概率是 \(\alpha\),一般取 \(\alpha = 95\%\)
迭代次数 \(N\):\(N\) 需保证 \(s\) 个点组成的随机样本中至少有一次没有野值的概率为 \(p\),一般取 \(p = 99\%\) \[ \begin{align} &N = \dfrac{\log{(1 - p)}}{\log{(1 - (1-\epsilon)^s)}} \\ \end{align} \] 其中 \(\epsilon\) 为样本中野值的比例;由于 \(\epsilon\) 一般未知,故可考虑用下面的自适应算法迭代求解: \[ \begin{align} &\text{init: }\text{N} = +\infty, \text{sample}\_\text{count} = 0 \\ &\textbf{while } \text{N} > \text{sample}\_\text{count}: \\ &\qquad \quad \text{draw a sample and count inner points} \\ &\qquad \quad \text{let }\epsilon = 1 - \dfrac{|\text{inner} \text{ points|}}{\text{|total samples|}} \\ &\qquad \quad \text{let }p = 99\% \text{ and calculate } \text{N} \\ &\qquad \quad \text{sample}\_\text{count} \leftarrow \text{sample}\_\text{count} + 1 \end{align} \]
一致集大小 \(T\):只要取 \(T\) 接近期望内点数量即可;对于 \(n\) 个样本,有 \(T = (1-\epsilon) n\)
算法流程:获得一个能够鲁棒拟合的模型
- 随机从 \(S\) 中选择 \(s\) 个数据点组成的样本作为模型的一个初始示例
- 确定在模型距离阈值 \(t\) 内的一个数据点集 \(S_i\),\(S_i\) 包含了模型的内点,称作采样的一致集
- 若 \(|S_i| > T\),说明该模型合理,用 \(S_i\) 内的所有点重估计模型(如最小二乘法)并结束
- 若 \(|S_i| \lt T\),说明该模型不合理,重抽一个新的子集 \(S_i'\) 并重复 a、b 步骤
- 若经过 \(N\)
次试验仍未终止,选择一个最大一致集 \(S_i\),并用 \(S_i\)
的所有点重估计模型(如最小二乘法)
注意:相较于 RANSAC,最小二乘法对离群点太敏感,难以在含野值的数据集上取得好的拟合效果
单应 \(\textbf{H}\) 的自动计算:输入两幅图像,输出单应的估计
在两幅图上分别计算兴趣点:兴趣点 = 图像自相关函数的极值点(纹理变化最显著的点)
根据兴趣点灰度领域接近程度,计算初始点对匹配集
用 RANSAC 求单应:重复 \(N\) 次采样,其中 \(N\) 可用上面的"自适应"算法迭代求解
- 任选 4 个样本(4 个点对),计算单应 \(\textbf{H}\)
- 对假设的每一组点对,计算距离 \(d\);其中 \(d^2 = d(\textbf{x}, \textbf{H}^{-1}\textbf{x}')^2 + d(\textbf{x}', \textbf{H}^{-1}\textbf{x})^2\),即对称转移误差
- 根据 \(d < t = \sqrt{5.99}\sigma\) 像素确定对应数量,也就是在 \(\textbf{H}\) 一致集内的内点数量
选择具有最大内点数量的 \(\textbf{H}\),作为迭代终止得到的单应
最优估计:对划定为"内点"的所有点对重新估计 \(\textbf{H}\)(最小化重投影误差)