『robotics-2』forward kinematics
正向运动学
一、D-H 参数法
什么是"正向运动学":已知开链机构各关节转角,求末端的位置和姿态
设置坐标系位置:
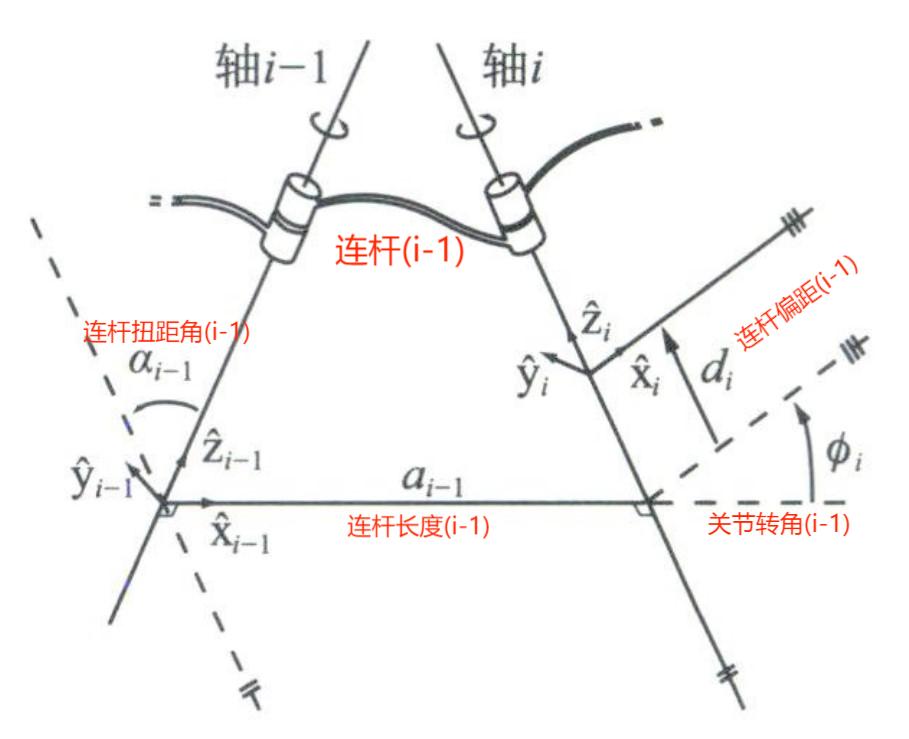
确定 轴\(i\) 的 \(\hat{z_i}\)轴:\(\hat{z}_i\) 的正方向与 关节轴\(i\) 的轴线重合,正方向由轴旋转下的右手螺旋定则确定
确定连杆坐标系的原点:设 \(\hat{z}_{i-1}\) 和 \(\hat{z}_{i}\) 有唯一的公法线,令该公法线连接轴 \(\hat{z}_{i-1}\) 和 轴 \(\hat{z}_i\)
系 {i-1} 的坐标原点就放在 轴i-1 和 公法线 的交点处(系 {i} 的原点暂时不确定)确定 \(\hat{x}\) 和 \(\hat{y}\) 的正方向:{i-1} 的 \(\hat{x}\) 常选在对应的公法线上,指向 轴i;{i-1} 的 \(\hat{y}\) 方向由右手系规范确定,即 \(\hat{x} \times \hat{y} = \hat{z}\)
注意:如果两个旋转轴相交导致公法线长度=0,任选一条平面\((\hat{z}_{i-1}, \hat{z_i})\)的法线即可;如果两个旋转轴平行,从无数条公法线中任选一条即可
定义 4 个参数:
连杆长度 \(a_{i-1}\):公法线的长度,即 \(\hat{z}_{i-1} \xrightarrow{\text{沿}\hat{x}_{i-1}\text{平移}}\hat{z}_i\) 的距离
注意:这里不应该望文生义,不是真实连杆的物理长度
连杆扭转角度 \(\alpha_{i-1}\): \(\hat{z}_{i-1} \xrightarrow{\text{绕} \hat{x}_{i-1}\text{旋转}} \hat{z}_i\) 的角度
连杆偏距 \(d_i\):从 \(\hat{x}_{i-1}\) 与 \(\hat{z}_i\) 的交点到连杆坐标系 {i} 原点的有向距离,即 \(\hat{x}_{i-1} \xrightarrow{\text{沿}\hat{z}_i\text{平移}} \hat{x}_i\) 的距离
关节转角 \(\phi_i\):\(\hat{x}_{i-1} \xrightarrow{\text{绕}\hat{z}_i旋转} \hat{x}_i\) 的角度
二、机器人正向运动学
齐次变换矩阵:由 D-H 参数决定变换矩阵 \(T_{i-1,i}\),每个连杆坐标系对应的齐次变换矩阵都有如下形式 \[ \begin{align} T_{i-1,i} &= \mathbf{Rot}(\hat{x}, \alpha_{i-1}) \mathbf{Trans}(\hat{x}, a_{i-1}) \mathbf{Trans}(\hat{z}, d_i)\mathbf{Rot}(\hat{z}, \phi_i) \\ &= \begin{bmatrix} \cos \phi_i & -\sin \phi_i & 0 & a_{i-1} \\ \sin \phi_i \cos \alpha_{i-1} &\cos phi_i \cos \alpha_{i-1} & -\sin \alpha_{i-1} & -d_i \sin \alpha_{i-1} \\ \sin \phi_i \sin \alpha_{i-1} & \cos \phi_i \sin \alpha_{i-1} & \cos \alpha_{i-1} & d_i \cos \alpha_{i-1} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \end{align} \]
旋转算子 1: \[\mathbf{Rot}(\hat{x}, \alpha_{i-1}) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha_{i-1} & -\sin \alpha_{i-1} & 0 \\0 & \sin \alpha_{i-1} & \cos \alpha_{i-1} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\]
平移算子 1: \[\mathbf{Trans}(\hat{x}, a_{i-1}) = \begin{bmatrix} 1 & 0 & 0 & a_{i-1} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]
平移算子 2: \[\mathbf{Trans}(\hat{z}, d_i) = \begin{bmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & d_i \\ 0 & 0 & 0 & 1 \end{bmatrix}\]
旋转算子 2: \[\mathbf{Rot}(\hat{z}, \phi_i) = \begin{bmatrix} \cos \phi_{i-1} & -\sin \phi_{i-1} & 0 & 0 \\ \sin \phi_{i-1} & \cos \phi_{i-1} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]
则该开链机构的正向运动学方程为 \(T_{0n}(\theta_1, \dots ,\theta_n) = T_{01}(\theta_1)T_{12}(\theta_2)\dots T_{n-1,n}(\theta_n)\)
\(T_{i-1,i}\) 表示相邻两个连杆 {i-1} 和 {i} 的相对位移齐次变换过程:从连杆坐标系{i-1} 变换到 连杆坐标系{i}
- 绕 {i-1} 的 \(\hat{x}\) 旋转 \(\alpha_{i-1}\)
- 沿 {i-1} 的 \(\hat{x}\) 平移 \(a_{i-1}\)
- 沿 {i} 的 \(\hat{z}\) 平移 \(d_{i}\)
- 绕 {i} 的 \(\hat{z}\) 旋转 \(\phi_i\)
三、实际算例
求解时额外需要注意的:
- 选取基坐标系:一般令 {0} 与 {1} 重合,保证当关节为转动副时 \(a_0 = \alpha_0 = d_1 = 0\),为移动副时 \(a_o = \alpha_0 = \phi_1 = 0\)
- 选取末端坐标系:一般把 {n} 放在末端执行器上的某个参考点
- 关节是移动副:坐标系设置方式与 转动副 不同
- \(\hat{z}\) 轴与移动副作用线方向相同(转动副的 \(\hat{z}\) 满足右手螺旋)
- 连杆偏距 \({d}\) 成为变量,关节转角 \({\phi}\) 成为常量(转动副则相反)
- 齐次变换的求解顺序:1 和 2 可颠倒,3 和 4 可颠倒
- \(\phi\) 转动的正方向:满足右手定则,大拇指沿轴方向,四指指向的方向是旋转正方向
例题:下面以空间开链RRRP机器人为例,同时包含移动副和转动副
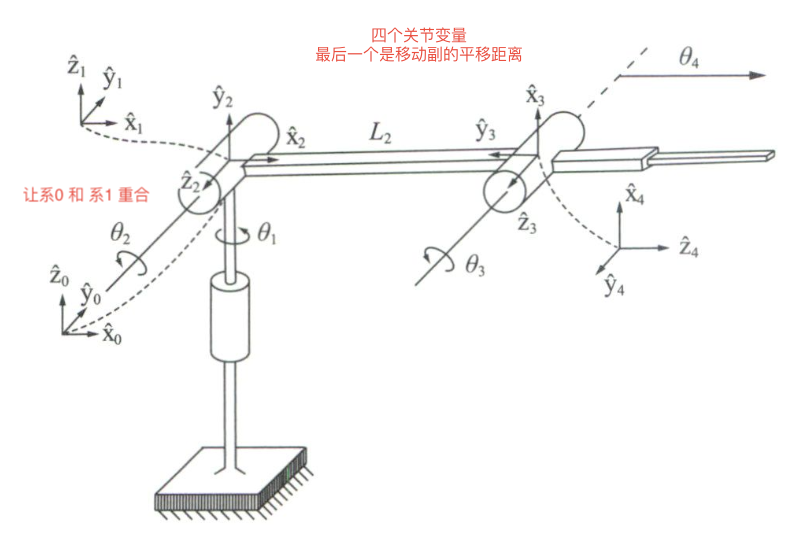

- 上表格中的 \((i, j)\) 表示从 {i-1} 到 {i} 需要经过 变换j
- 变换j 的值是在经过 变换j-1 后才求出的(不是开始时一次性量出的)
- 对于填充最后一个变量 \(\phi\),保持 {i-1} 不动、先把 {i} 旋转 \(\phi_i\) 度,再看把 {i-1} 绕\(\hat{z}_i\)旋转多少度可得到 {i}