『cyber security-2』asymmetric encryption

公钥密码体系

一、非对称加密概述

• 非对称加密方法：用两个不同的密钥进行加密 or 解密

• 两个密钥：公钥 + 私钥

  • 公开密钥：公开的，可用于加密 + 验签
  • 私有密钥：秘密的，可用于解密 + 签名

• 非对称的内涵：用于 加密 + 验签 的密钥 无法 解密 or 签名

• 公钥算法的条件：加密可行 + 破密不可行

  • 加密可行：
    • 产生一对密钥是计算可行的
    • 已知公钥 + 明文，产生密文是计算可行的
    • 接收方利用私钥解密是计算可行的
  • 破密不可行：
    • 利用公钥推断私钥是计算不可行的
    • 已知公钥和密文，破解明文是计算不可行的

• 公钥加密的用途

  • 密钥分发：共享对称密钥
  • 数字签名：商业和个人应用

  注意：公钥密码不一定比对称密钥更安全（取决于密钥长度）；且公钥密码计算开销很大，暂时难以取代传统密码

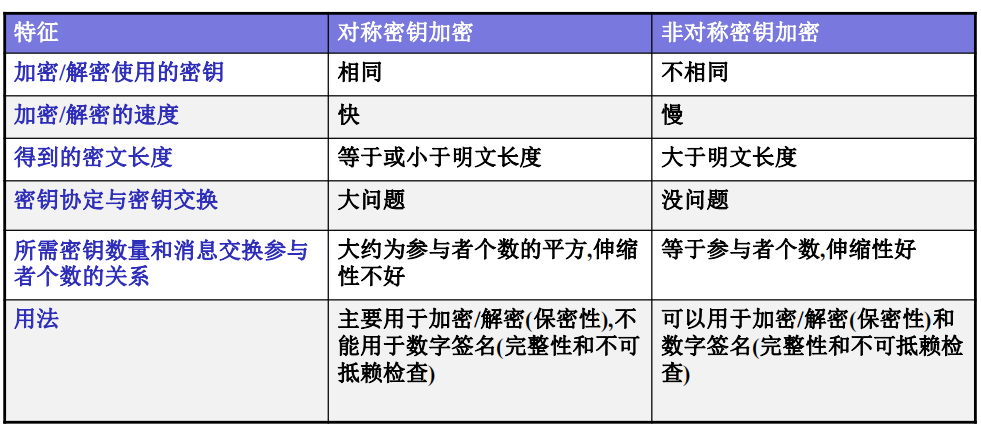
• 对称密钥加密 VS. 非对称密钥加密：

  

---

二、RSA算法

• 算法描述：大整数素因子分解系统，由图灵奖得主 Ronald L. Rivest + Adi Shamir 发明

  • RSA是应用最广泛的公钥密码算法
  • 一种分组密码，其明文和密文均为 0 ~ n-1 之间的整数（mod n）。

• 产生密钥对：选择两个大素数p和q，p \(\ne\) q

  • 计算 \(n = pq\) 和 欧拉函数 \(\phi(n) = (p-1)(q-1)\)
  • 选择整数e，使得 \(\gcd(e, \phi(n)) = 1\)
  • 选择整数d，使得 \(d e \text{ mod } \phi(n) = 1\)
  • 公钥KU = \(\{e, n\}\)，私钥KR = \(\{d, n\}\)

• 算法流程：设明文分组为M，密文分组为C；收发双方均知道 n 和 e（即公钥），但只有接收方知道 d（即私钥）

  • 加密：\(\text{C} = \text{M}^\text{e} \text{ mod } n\)
  • 解密：\(\text{M} = \text{C}^\text{d} \text{ mod } n = \text{M}^{\text{ed}} \text{ mod } n\)

• RSA算法需要满足的三个条件：加解密 + 难破解

  • 能够找到 e、d、n 使得 \(\text{M}^{\text{ed}} \text{ mod } n = \text{M}\)（\(\text{M} < n\)）
  • 计算 \(\text{M}^\text{e}\) 和 \(\text{C}^\text{d}\) 相对容易
  • 从 e 和 n （公钥）得到 d （私钥）是在计算上不可行的（所以应使 e 和 n 的值尽可能大）

• RSA安全性分析：破解方法主要包括 蛮力攻击 + 素因子分解攻击 + 选择密文攻击

  • 已知的破解方法至少跟因子分解难度相同：将大数 n 分解为两个素因子很困难
    • 因子分解：将 n 分解为两个素因子p和q \(\Rightarrow\) 计算 \(\phi(n) = (p-1) \times (q-1)\) \(\Rightarrow\) \(d \equiv e^{-1}\)(mod \(\phi(n)\))
    • 另解：直接确定\(\phi(n)\)，或直接确定 d
  • 尚未发现多项式时间的因子分解算法
  • 512位的RSA已被证明是不安全的

  注意：\(a \equiv b\) (mod) \(n\) 指的是 \(a\) 除以 \(n\) 余数为 \(b\)

• 如何提高RSA安全性？

  • 选择足够大的 n（512bit已经不安全了）
  • e 和 d 相差不太大，也不太小
  • p 和 q 长度仅相差几位

---

三、国产密码算法

• 用途：保障商用密码（SM）的安全性

• 分类：主要包含 SM1、SM2、SM3、SM4、SM7，由国家密码局制定标准

  • SM1：算法不公开，要调用专用加密芯片的接口
    • 对称密码
    • 分组密码，分组长度为128bit
    • 用于研制智能IC卡、智能密码钥匙、加密卡或加密机器等安全产品（政务通、警务通）
  • SM2：算法已公开
    • 非对称密码，属于椭圆曲线密码机制（ECC）
    • 多方面优于RSA（比RSA更新）
    • 用于数字签名、密钥交换协议和公钥加密算法
  • SM3：算法已公开
    • 类似MD5，使用Hash生成长度为256bit的摘要（或称杂凑值）
    • 用于数字签名和验证，消息验证码生成和验证、随机数生成
  • SM4：算法已公开
    • 对称密码
    • 分组密码，分组长度为128bit；密钥长度为128bit
    • 采用Feistel结构的分组密码算法（见对称加密算法），解密与加密结构相同
    • 用于无线局域网产品
  • SM7：算法不公开，要调用专用加密芯片的接口
    • 分组密码，分组长度为128bit；密钥长度为128bit
    • 用于非接触式IC卡、工作门禁等身份识别应用、票务类应用

  ---

  四、Diffie-Hellman算法

  • 素数的原根：设大素数是\(p\)，若\(a\)是素数\(p\)的原根，则 \(a^1\) mod \(p\), ..., \(a^{p-1}\) mod \(p\) 各不相同，且是 1 ~ p-1 的一个置换

  • 密钥交换算法：设素数\(p\)和其本原根为\(a\)，都是公开的；A和B意图交换密钥

    1. A设置私钥，交换公钥（握手）：A选择一个随机整数\(X_A < p\)，并计算 \(Y_A = a^{X_A}\) mod \(p\)，把 \(Y_A\) 发送给B
    2. B设置私钥，交换公钥（握手）：B选择一个随机整数\(X_B < p\)，并计算\(Y_B = a^{X_B}\) mod \(p\)，把 \(Y_B\) 发送给A
    3. A计算共享密钥：根据B发来的\(Y_B\)，求得 \(K = (Y_B)^{X_A}\) mod \(p\)
    4. B计算共享密钥：根据A发来的\(Y_A\)，求得 \(K = (Y_A)^{X_B}\) mod \(p\)

  • DH算法安全性分析：有限域中离散对数计算的困难性

    • 求模指数：\(Y_B = a^{X_B}\) mod \(p\)，较容易
    • 求一个数的离散对数：找出 \(X_B\) 使得 \(Y_B = a^{X_B}\) mod \(p\)，很困难

  • 中间人攻击：DH算法对中间人攻击并不安全，中间人可能跟A共享一个密钥\(K_2\)、而跟B共享一个密钥\(K_1\)

    

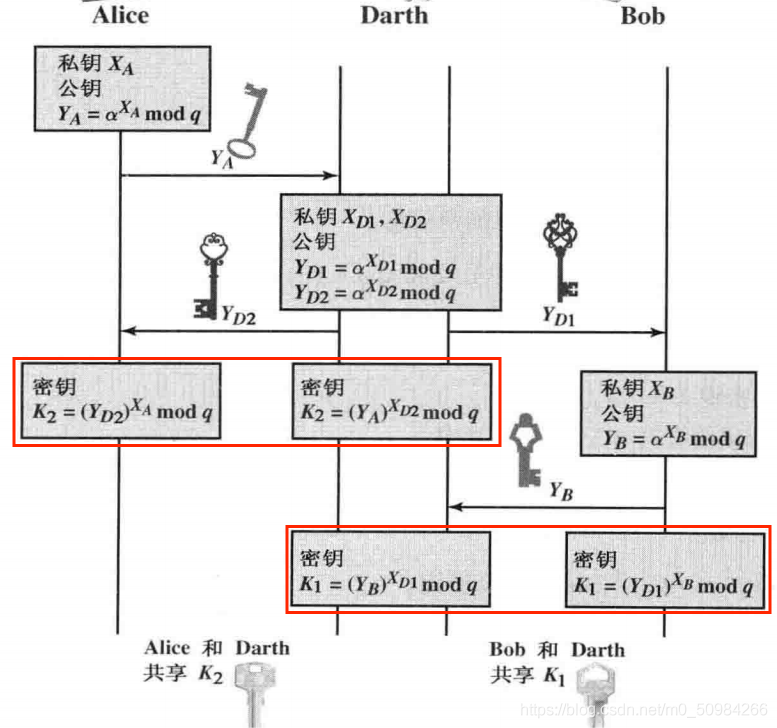
    • 攻击方式：

      • 窃听风险：A向中间人发送加密消息\(E(K_2, M)\)，中间人使用\(K_2\)恢复并窃听消息\(M\)
      • 重放风险：中间人截获并恢复了\(E(K_2, M)\)，并向B发送了篡改后的\(E(K_1, M')\)
      • 暴力破解：客户端私钥随机生成，而服务器方私钥固定 \(\Rightarrow\) 依据海量密钥协商数据暴力破解服务器私钥

    • 解决方法：双方私钥在每次进行密钥交换通信时，都是随机生成的临时私钥，也称DHE算法（Ephemeral，临时性的）

    • ECDHE：基于椭圆曲线的密钥交换算法，在DHE的基础上利用ECC椭圆曲线特性

      • 特点：支持前向安全性（破解当前的密钥，则之前的加密数据也会被破解）

        注意：RSA算法不支持前向安全性

      • 工作流程：

        1. 客户端和服务端各随机选择一个椭圆曲线私钥，并生成椭圆曲线公钥
        2. 握手阶段，双方交换椭圆曲线公钥
        3. 双方各自使用自己的私钥 + 对方的公钥 通过椭圆曲线运算 生成共享密钥