『signal and system-3』Fourier transform
傅里叶变换
一、傅里叶级数
傅立叶级数的非复数表达形式:设 \(x(t)\) 以 \(T_0\) 为周期,则有 \[ \begin{align} &x(t) = B_0 + \sum_{k=1}^\infty B_k \cos(k \omega_0 t) + \sum_{k=1}^\infty C_k \sin(k \omega_0 t) \\ &\text{其中} \begin{cases} B_0 = \frac{1}{T_0} \int_0^{T_0} x(t) dt \\ \\ B_k = \frac{2}{T_0} \int_{0}^{T_0} x(t) \cos(k \omega_0 t) dt \\ \\ C_k = \frac{2}{T_0} \int_{0}^{T_0} x(t) \sin(k \omega_0 t) dt \\ \end{cases} \end{align} \]
注意:若 \(x(t)\) 为偶函数,最后一项必然=0;若 \(x(t)\) 为奇函数,前两项之和必然=0
傅立叶级数的复数表达形式:更简洁,更常用,与上面的表述等价 \[ \begin{align} &x(t) = \sum_{k=-\infty}^{+\infty} a_k e^{jk\omega_0 t} \\ &\text{其中 } a_k = \frac{1}{T_0} \int_0^{T_0} x(t) e^{-jk\omega t} dt \text{,} \omega_0 = \frac{2 \pi}{T_0} \\ \end{align} \] 其中 \(\omega_0\) 是基波频率,\(T_0 = \dfrac{2 \pi}{T_0}\) 是基波周期
两种傅立叶级数间的转换关系:互相可推导 \[ \begin{cases} B_0 = a_0 \\ \\ B_k = a_{-k} + a_k \\ \\ C_k = j(a_k - a_{-k}) \\ \end{cases} \text{ }\text{ }\text{ }\text{ } \begin{cases} a_0 = B_0 \\ \\ a_k = \frac{1}{2} (B_k - jC_k) \\ \\ a_{-k} = \frac{1}{2} (B_k + jC_k) \\ \end{cases} \]
二、函数的正交分解
内积运算:设二元运算 \(<.,.>\) 满足以下性质:
- 交换律:\(<x, y> = \overline{<y, x>}\),即交换运算顺序等于其共轭
- 齐次性:\(<\lambda x, y> = \lambda<x, y>\)
- 叠加性:\(<x + y, z> = <x,z> + <y + z>\)
- 非负性:\(<x, y> = 0 \Leftrightarrow x = y\),\(<x, y> \ge 0\)
信号的内积运算:
- 连续信号:\(<x(t), y(t)> = \int_{a}^{b} x(t) \overline{y(t)} dt\)
- 离散信号:\(<x[n], y[n]> = \sum_{k = a}^{k = b}x[n]\overline{y[n]}\)
正交函数族:设函数族为 \(\{e_k\}_{k=1, \dots , +\infty}\),则该函数族为正交函数族 \(\Leftrightarrow\) \(\forall k_i \ne k_j, <e_{k_i}, e_{k_j}> = 0\),且 \(\forall k, <e_k, e_k> \ne 0\)
该定义下的函数内积为 \(<x(t), y(t)> = \int_{T_0} x(t)\overline{y(t)} dt\),即任意基波周期下的内积运算注意:"正交函数族"的定义严格依赖于"内积运算"的定义
标准正交基函数:设函数族为 \(\{e_k\}_{k=1, \dots ,+\infty}\),则该函数族为标准正交基函数族 \(\Leftrightarrow\) \(\forall k_i \ne k_j, <e_{k_i}, e_{k_j}> = 0\),且 \(\forall k, <e_k, e_k> = 1\)
正交基标准化:\(e_k' = \dfrac{e_k}{\sqrt{<e_k, e_k>}}\),可保证不同函数间内积为0,同时相同函数自己内积结果标准化为1
例:使用正交基推导傅立叶级数的复数形式
证明 \(\{e^{jk\omega_{0} t}\}_{k=1,\dots,\infty}\) 为正交基: \[ \begin{align} &\text{同一函数自内积: }<e^{jk\omega_0 t}, e^{jk\omega_0 t}> = \int_{0}^{T_0} e^{jk\omega_0t} \overline{e^{jk\omega_0t}} dt = \int_{0}^{T_0} e^{jk\omega_0 t} e^{-jk\omega_0 t} dt = T_0 > 0 \\ &\text{不同函数做内积:}<e^{jk_1\omega_0t}, e^{jk_2\omega_0t}> = \int_{0}^{T_0} e^{jk_1\omega_0 t} \overline{e^{jk_2\omega_0 t}} dt = \int_{0}^{T_0} e^{j(k_1-k_2)\omega_0t} dt = e^{j(k_1-k_2)\omega_0T_0} - 1 = e^{2jk\pi} - 1 = 0 \end{align} \]
求解 \(x(t)\) 展开级数的系数 \(a_k\): \[ \begin{align} &\text{求谁就“跟谁内积”:}<x(t), e^{jk\omega_0 t}> = <\sum_{u=-\infty}^{+\infty} a_u e^{ju\omega_0t}, e^{jk\omega_0 t}> \\ &\text{由内积的叠加性:} <\sum_{u=-\infty}^{+\infty} a_u e^{ju\omega_0t}, e^{jk\omega_0 t}> = \sum_{u=-\infty}^{+\infty} <a_ue^{ju\omega_0 t}, e^{jk\omega_0 t}> = T_0a_k \\ &\text{故 }a_k = \dfrac{<x(t), e^{jk\omega_0t}>}{T_0} = \dfrac{1}{T_0} \int_{T_0} x(t) \overline{e^{jk\omega_0 t}} dt = \dfrac{1}{T_0} \int_{T_0} x(t) e^{-jk\omega_0t} dt \text{ ,证毕。} \end{align} \]
正交基函数:
Fourier 正交基:\(\{1\} \cup \{\cos (k\omega_0x)\}_{k=1, \dots+\infty} \cup \{\sin (k\omega_0x)\}_{k=1, \dots ,+\infty}\)
Legendre 多项式:\(P_n(x) = \dfrac{1}{2^n n!} \dfrac{d^n[(x^2 - 1)^n]}{dx^2}\);表示 \([-1, +1]\) 上的函数 \(f(x) = \sum_{k=1}^{+\infty} a_k P_k(x)\) \[ \begin{align} &\text{与自身做内积:} \int_{-1}^{+1} [P_n(x)]^2 dx = \dfrac{2}{2n + 1} > 0 \\ &\text{两不同函数内积:} \int_{-1}^{+1} P_m(x)P_n(x) dx = 0 \text{ }\text{ }(m \ne n) \\ \end{align} \]
Haar 小波:短时域上的方波
三、傅里叶变换
傅里叶正逆变换的推导:定义 \(X(j\omega) = \int_{T_0} x(t) e^{-j\omega t}dt\),则有 \(a_k = \dfrac{1}{T_0} \int_{T_0} x(t) e^{-jk\omega_0 t} dt = \dfrac{1}{T_0} X(jk\omega_0)\) \[ \begin{align} &\text{则原傅里叶级数可改写为:} x(t) = \sum_{k=-\infty}^{+\infty} a_k e^{jk\omega_0t} = \dfrac{1}{\omega_0T_0} \sum_{k=-\infty}^{+\infty} X(jk\omega_0) e^{jk\omega_0} \omega_0 = \dfrac{1}{2\pi}\sum_{k=-\infty}^{+\infty} X(jk\omega_0) e^{jk\omega_0} \omega_0\\ & \text{将傅里叶级数推广到}\textbf{非周期}\text{函数上:令 }T_0 \rightarrow +\infty \text{ ,则 }{\omega_0} \rightarrow 0 \\ &\text{由黎曼积分定义:}x(t) = \dfrac{1}{2\pi} \int_{-\infty}^{+\infty} X(j\omega)e^{j\omega t} d\omega \\ &\text{结合上述推导:}\begin{cases} X(j\omega) = \int_{-\infty}^{+\infty} x(t) e^{-j\omega t} dt \text{ (正变换)} \\ \\ x(t) = \dfrac{1}{2\pi} \int_{-\infty}^{+\infty} X(j\omega) e^{j\omega t} d\omega \text{ (逆变换)} \end{cases} \end{align} \] 其中 \(x(t)\) 为时域、\(X(j\omega)\) 为频域;记傅里叶变换为 \(x(t) \xrightarrow{F} X(j\omega)\),逆变换为 \(X(j\omega) \xrightarrow{F^{-1}} x(t)\)
注意:傅里叶变换揭示了同一个信号 时域 和 频域 之间的互相转换关系
典型信号的傅里叶变换:
\(e^{-at}u(t) \xrightarrow{F} \dfrac{1}{a + j\omega}\)(\(a > 0\)),又称 "低通滤波器":只允许频率绝对值小的通过,频率大的被抑制
推导过程:按 Fourier 变换的定义积分即可 \[ \begin{align} X(j\omega) = \int_{-\infty}^{+\infty} x(t) e^{-j\omega t} dt = \int_{0}^{+\infty} e^{-at} \times e^{-j\omega t} dt = \dfrac{1}{a + j\omega}\text{ ,证毕。} \end{align} \]
模长-相位图:一般将信号拆解为 \(X(j\omega) = |X(j\omega)| \theta(j\omega)\),前者为 Amplitude,后者为 Phase
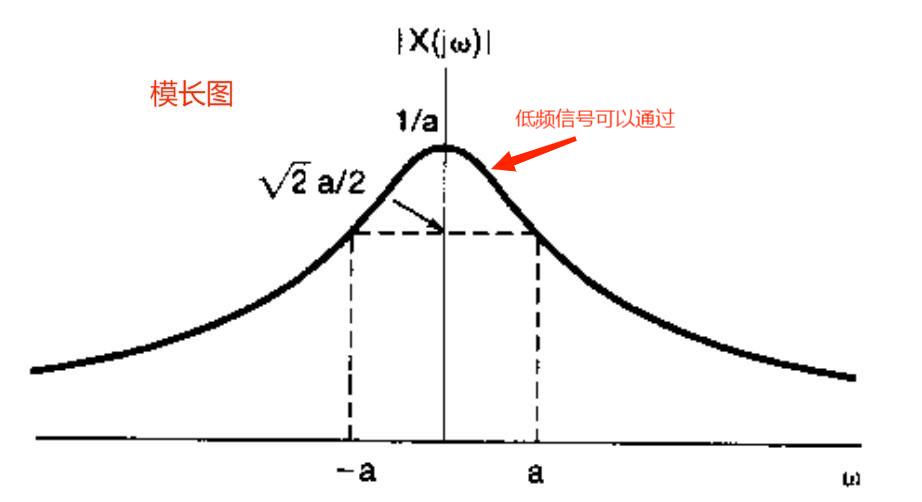
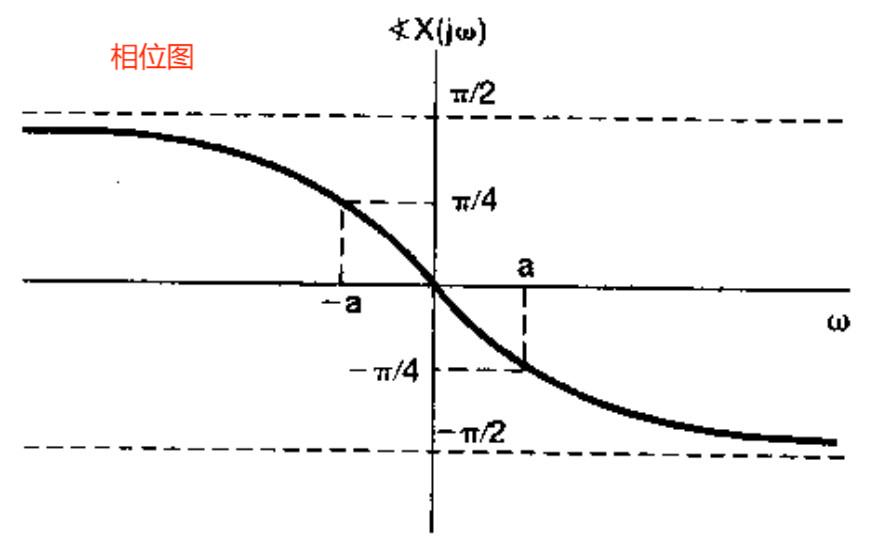
注意:对于复数 \(a + bj\),其模长=\(\dfrac{1}{\sqrt{a^2 + b^2}}\),相位 \(\theta\)=\(\arctan{\dfrac{b}{a}}\)
\(\delta(t) \xrightarrow{F} 1\),\(1 \xrightarrow{F} 2\pi \delta(\omega)\)
- 推导过程: \[ \begin{align} \text{左式推导:} &X(j\omega) = \int_{-\infty}^{+\infty} x(t) e^{-j\omega t} dt = \int_{-\infty}^{+\infty} \delta(t) e^{-j\omega t} dt \\ &\text{由 } \int_{-\infty}^{+\infty} x(t) \delta(t) dt = x(0) \text{ ,} \int_{-\infty}^{+\infty} \delta(t) e^{-j\omega t} dt = e^{-j \omega \times 0} = 1 \\ \text{右式推导:} &X(j\omega) = \int_{-\infty}^{+\infty} e^{-j \omega t} dt = \lim_{N \rightarrow +\infty} \int_{-N}^{+N} e^{-j \omega t} dt = \lim_{N \rightarrow +\infty} \dfrac{1}{j\omega} ({e^{j\omega N} - e^{-j\omega N}}) \\ &= \lim_{N \rightarrow +\infty} \dfrac{1}{j\omega} {2j \sin(\omega N)} = 2 \lim_{N \rightarrow +\infty} \dfrac{\sin(\omega N)}{\omega} = 2\pi \delta(\omega) \text{ ,证毕。} \end{align} \]
\([-\dfrac{\tau}{2}, \dfrac{\tau}{2}]\text{ 上值为 }E\text{ 的方波} \xrightarrow{F} E \tau (Sa(\omega \dfrac{\tau}{2})) = \dfrac{2E\sin(\omega \dfrac{\tau}{2})}{\omega}\),其中 \(Sa\) 指采样函数
- 推导过程: \[ \begin{align} X(j\omega) &= \int_{-\dfrac{\tau}{2}}^{+\dfrac{\tau}{2}} E e^{-j\omega t} dt = E \times \dfrac{1}{j\omega} (e^{j\omega \dfrac{\tau}{2}} - e^{-j\omega \dfrac{\tau}{2}}) \\ &=E \times \dfrac{1}{j\omega} \times 2j\sin(\omega \dfrac{\tau}{2}) = \dfrac{2E\sin(\omega \dfrac{\tau}{2})}{\omega} \text{ ,证毕。} \end{align} \]
\(\dfrac{\sin(\omega_c t)}{\pi t} \xrightarrow{F}\) \([-\omega_c, \omega_c]\) 上 值为 1 的方波
- 推导过程: \[ \begin{align} X(j\omega) &= \int_{-\infty}^{+\infty} \dfrac{\sin(\omega_c t)}{\pi t} e^{-j\omega t} dt = \int_{-\infty}^{+\infty}\dfrac{\sin(\omega_c t)}{\pi t} [\cos(\omega t) - j\sin(\omega t)] dt \\ &= \int_{-\infty}^{+\infty} \dfrac{\sin(\omega_c t)}{\pi t}\cos(\omega t) dt - j\int_{-\infty}^{+\infty}\dfrac{\sin(\omega_c t)}{\pi t}\sin(\omega t) dt = \int_{-\infty}^{+\infty} \dfrac{\sin(\omega_c t)}{\pi t}\cos(\omega t) dt - 0\\ \text{由积化和差}&=\dfrac{1}{2} [\int_{-\infty}^{+\infty}\dfrac{\sin(\omega_c + \omega)t}{\pi t} dt + \int_{-\infty}^{+\infty} \dfrac{\sin(\omega_c - \omega)t}{\pi t} dt ]\\ \text{由已知结论}&\int_{-\infty}^{+\infty} \dfrac{\sin(\omega t)}{\pi t} = \begin{cases} 1 & \text{when } \omega > 0 \\ \\ -1 & \text{when } \omega < 0 \end{cases} \text{ }\text{ 故考虑对 }\omega \text{ 的取值范围讨论} \\ &\text{若 }\omega < -\omega_c \text{,则 }\omega + \omega_c < 0, \text{ }\omega_c - \omega > 0 \Rightarrow X(j\omega) = \dfrac{1}{2} (-1+1) = 0 \\ &\text{若 }-\omega_c < \omega < \omega_c \text{,则两项都=1} \Rightarrow X(j\omega) \dfrac{1}{2} (1 + 1) = 1 \\ &\text{若 }\omega > \omega_c \text{ ,则 }X(j\omega) = \dfrac{1}{2} (1-1) = 0 \text{ ,证毕。} \end{align} \]