『signal and system-1』about signal
信号与系统
一、信号是什么
- 信号是表达信息的符号,包含一维信号(传递声音信息)、二维信号(传递图像信息)等等。
二、信号的分类
连续时间信号:自变量连续可变的信号,用 t 表示连续时间变量,记作 x(t)
离散时间信号:自变量仅取在一组离散值上,用 n 表示离散时间变量,记作 x[n]
注意:离散信号用方括号 [ . ] 表示,连续信号用圆括号 ( . ) 表示
周期信号:信号随时间变量 t 或 n 变化,具有重复性
- 连续周期信号:存在一个正值 T,对于全部连续 t 满足 x(t) = x(t + T),并记最小正周期为基波周期 \(T_0\)
- 离散周期信号:存在一个正值 T,对于全部离散 n 满足 x[n] = x[n + N],并记最小正周期为基波周期\(N_0\)
奇信号:信号关于原点对称,满足 x(t) = -x(-t),或 x[n] = -x[-n]
偶信号:信号关于坐标纵轴对称,满足 x(t) = x(-t),或 x[n] = x[-n]
注意:任何信号都能被唯一地分解为两个信号之和,满足一个是奇信号,另一个是偶信号
设 x(t) 是任意连续时间信号,则 \(\text{x(t)} = \dfrac{1}{2}\text{[x(t) + x(-t)]} + \dfrac{1}{2}[\text{x(t)} - \text{x(-t)}]\),前者是偶信号,后者是奇信号
三、信号的能量和功率
一段有限时间内的信号总能量和平均功率:设时间段为 \(n_1 \le n \le n_2\)
离散信号的总能量:\(E = \sum_{n = n_1}^{n=n_2} |{x[n]}|^2\),即对信号模长的平方求和
离散信号的平均功率:\(P = \dfrac{1}{n_2 - n_1 + 1}\sum_{n=n_1}^{n=n_2}|x[n]|^2\),即对能量计算平均值
连续信号的总能量:\(E = \int_{t_0}^{t_1} |x(t)|^2 dt\),即对信号模长的平方求积分
连续信号的平均功率:\(P = \dfrac{1}{t_1 - t_0} \int_{t_0}^{t_1} |x(t)|^2 dt\),即对能量计算平均值
注意:有限时间可以推广到无限时间段,令 \(n_1 \rightarrow - \infty\),或 \(n_2 \rightarrow \infty\) 即可
单位阶跃信号:记作 u(t),小于 0 时取 0,大于 0 时取 1,u(0) 可取任意值 \[ u(t) = \begin{cases} 1 & \text{if } t > 0 \\ 0 & \text{if } t < 0 \\ \text{any} & \text{if } t = 0\\ \end{cases} \]
冲激信号:记作 \(\delta(t)\),用于表示一种发生时间极短、但物理量取值极大的物理现象(雷电、冲击力等) \[ \begin{align} \delta(t) = \begin{cases} +\infty & \text{if } t = 0 \\ 0 & \text{other} \\ \end{cases} \\ \text{ 同时满足} \int_{-\infty}^{+\infty} \delta(t) dt = 1 \end{align} \]
注意:以上两个函数满足关系:\(\delta(t) = \dfrac{du(t)}{dt}\),即冲激信号是单位阶跃信号的导函数(t = 0 时冲到最高)
抽样函数:记作 Sa(t),是一个偶函数,t = 0 处取极限值 1 \[ Sa(t) = \begin{cases} 1 & \text{if } t = 0 \\ \dfrac{\sin(t)}{t} & \text{other} \end{cases} \]
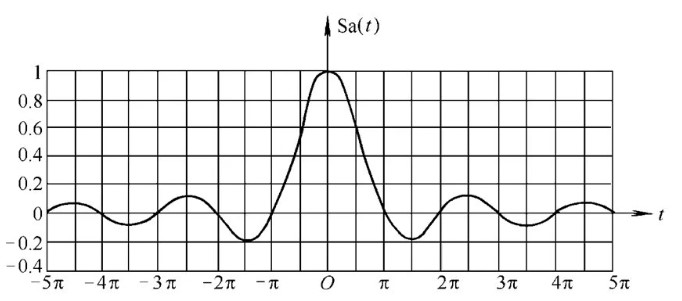
抽样函数图像
注意:\(\int_{-\infty}^{+\infty} \dfrac{\sin{(t)}}{t} dt =\int_{-\infty}^{+\infty} \dfrac{\sin(\omega t)}{t} = \pi\)(\(\omega > 0\)), \(\int_{0}^{+\infty} \dfrac{\sin(t)}{t} dt = \int_{-\infty}^0 \dfrac{\sin(\omega t)}{t} dt = \dfrac{\pi}{2}\)(\(\omega > 0\))
关于以上抽样函数结论的证明:偶函数性质 + 欧拉公式的应用 \[ \begin{align} &先证明 \int_{0}^{+\infty} \frac{\sin(t)}{t} dt = \frac{\pi}{2} \text{:} \\ &\text{设 } I(a) = \int_{0}^{+\infty} \frac{\sin(t)}{t} e^{-at} dt \text{ ,则 } \frac{dI(a)}{da} = -\int_{0}^{+\infty} {\sin(t)} e^{-at} dt \\ &\text{由 } \sin(t) = \frac{e^{it} - e^{-it}}{2i},可将上式转化为\text{:} \\ &-\frac{1}{2i} \int_{0}^{+\infty} e^{-(a + i)t} - e^{-(a-i)t} dt = \frac{1}{2i} [\frac{1}{a+i} - \frac{1}{a-i}] = -\frac{1}{a^2 + 1} \\ &\text{即 } \frac{dI(a)}{da} = -\frac{1}{a^2 + 1} \text{,查积分表可得 } I(a) = -\arctan(a) + C \\ &\text{令 } a \rightarrow +\infty \text{,可得 } I(a) = 0 = -\frac{\pi}{2} + C\text{ ,解得 } C = \frac{\pi}{2} \\ &\text{最后令 }a = 0\text{,解得原积分 = } \frac{\pi}{2},证毕。 \end{align} \]
单位阶跃序列:记作 u[n],可理解为离散形式的单位阶跃信号;注意 n = 0 时取 1(而非连续形式的任意值) \[ u[n] = \begin{cases} 0 & \text{if } n < 0 \\ 1 & \text{other} \\ \end{cases} \]
单位脉冲序列:记作 \(\delta\)[n],可理解为离散形式的冲激信号;注意 n = 0 时取 \(\delta\)[n] = 1(而非连续形式的正无穷) \[ \delta[n] = \begin{cases} 1 & \text{if } n = 0 \\ 0 & \text{other} \end{cases} \]
四、自变量变换
对于连续信号 x (t),求解任意形如 x(at + b) 的连续信号:
- 化成标准型:\(x(t) \rightarrow x(a(t + \dfrac{b}{a}))\),即把变量 t 前的系数提成 1
- 系数为负则翻转:若 a < 0,则需要将 x(t) 的图像先沿 纵轴 对称翻转
- 系数 > 1 压缩,系数 < 1 拉伸:将(对称翻转过的)每个信号点横坐标 t 平移到 \(\dfrac{t}{|a|}\) 处
- 加号左移,减号右移:若 b > 0,图像总体左移 b 个单位;若 b < 0,图像总体右移 |b| 个单位
有关自变量变换的重要结论:\(x[n] = \sum_{k = -\infty}^{+\infty} x[k] \text{ }\delta[n-k]\),其中 \(\delta[n-k]\) 表示仅在 n = k 处取值为1的信号
例:根据自变量变换的规律求解 u[n + p] - u[n - q] 的图像(p, q > 0);根据 x(at + b) 的图像反推 x(t) 的图像(令 u = at + b)
五、线性系统
线性系统的定义:同时满足以下两个性质的系统称作"线性系统"
- 齐次性:设系统 \(x(t) \rightarrow y(t)\),则对任意 \(a \in \mathbb{R}\) ,都有 \(ax(t) \rightarrow ay(t)\)
- 叠加性:设系统 \(x_1(t) \rightarrow y_1(t)\)、\(x_2(t) \rightarrow y_2(t)\),则必有 \(x_1(t) + x_2(t) \rightarrow y_1(t) + y_2(t)\)
注意:对于离散信号系统,只需要把 (t) 替换成 [n] 即可
常见的线性系统:证明一个系统是线性系统,需同时验证"齐次性"和"叠加性";证明不是线性系统,只需给出反例
- 缩放器:连续情形有 \(x(t) \rightarrow ax(t)\);离散情形有 \(x[n] \rightarrow ax[n]\)
- 微分器:连续情形有 \(x(t) \rightarrow \dfrac{dx(t)}{dt}\);离散情形有 \(x[n] \rightarrow x[n] - x[n-1]\)
- 积分器:连续情形有 \(x(t) \rightarrow \int_{-\infty}^{t} x(\tau) d\tau\);离散情形有 \(x[n] \rightarrow \sum_{k = -\infty}^{n} x[k]\)
注意:系统的每一项都含信号 x,且每一项的 x 都是一次幂 \(\Rightarrow\) 该系统是线性系统,
六、时不变系统、因果系统、无记忆系统等
时不变系统:设系统 \(x(t) \rightarrow y(t)\),对任意 \(t_0 \in \mathbb{R}\),都有 \(x(t-t_0) \rightarrow y(t-t_0)\),即系统输出不随时间改变
注意:t 只存在于信号 x 的括号内,且 t 总以单独形式存在(不带系数、不是幂次等)\(\Rightarrow\) 该系统是时不变系统
因果系统:设系统 \(x(t) \rightarrow y(t)\),输出 \(y(t)\) 始终在输入 \(x(t)\) 之后发生,即系统的输出只与当前和过去的输入有关
- 微分器 \(y(t) = \dfrac{dx(t)}{dx}\) 既可以看作是因果的(左极限),也可以看作非因果的(右极限)
注意:信号 x 括号内的关于 t 的表达式 恒 \(\le\) t \(\Rightarrow\) 该系统是因果系统(输出总是落后于输入)
无记忆系统:设系统 \(x(t) \rightarrow y(t)\),\(y(t)\) 的值仅仅只依赖于 \(x(t)\) 的值(而不依赖于 x(t-1) 等)
- 微分器 \(y(t) = \dfrac{dx(t)}{dx}\) 其实是有记忆的,因为导数的极限定义是 \(\lim_{\Delta t \rightarrow 0} \dfrac{x(t + \Delta t) - x(t)}{\Delta t}\)
注意:信号 x 与 y 括号内的值完全一样 \(\Rightarrow\) 该系统是无记忆的(仅依赖于输入信号\(x(t)\))
一个系统是无记忆的 \(\Rightarrow\) 该系统是因果的(无记忆 是 因果 的特殊情况)
可逆系统:设系统 \(x(t) \rightarrow y(t)\),\(x(t)\) 能唯一地写成 \(y(t)\) 的形式,即可以用输出信号唯一地表示输入信号
\(x(t) \rightarrow y = x^2(t)\) 是不可逆的,因为 \(x(t) = \pm \sqrt{y(t)}\),\(x(t)\) 有两种被 \(y(t)\) 表示的方法
\(x(t) \rightarrow y(t) = \int_{-\infty}^{t} x(\tau) d\tau\) 是可逆的,因为 \(x(t) = \dfrac{dy(t)}{dt}\),表示方法唯一
注意:积分器(累加器)是可逆的,微分器是不可逆的(积分常数 C 可取任意值)
稳定系统:设系统 \(x(t) \rightarrow y(t)\),若 \(x(t)\) 有界则 \(y(t)\) 有界,说明该系统稳定,即输入有界则输出有界
\(y(t) = \dfrac{dx(t)}{dt}\) 是不稳定的,比如取 \(x(t) = u(t)\)(有界),\(y(t)\) 在 t = 0 处 \(\rightarrow +\infty\) 没有界
\(y(t) = \int_{-\infty}^{t} x(\tau) d\tau\) 是不稳定的,比如取 \(x(t) = 1\)(有界),\(y(t) \rightarrow +\infty\) 没有界
\(y[n] = x[n] - x[n - 1]\) 是稳定的,设 \(|x[n]| \le M\),则 \(|y[n]| \le 2M\)(\(M > 0\)),即离散信号作差必有界
\(y[n] = \sum_{k = -\infty}^{n} x[k]\) 是不稳定的,证明与连续情形的积分器相同