『cyber security-1』encryption algorithm

密码算法

一、对称加密原理

  • 对称加密方案的5个组成部分：

    • 明文：加密算法的输入，属于原始可理解的消息和数据
    • 加密算法：用于对明文进行各种代换和变换的算法
    • 密钥：加密算法的参数（与明文一样都是算法的输入），算法所使用的特定代换和替代依赖于密钥
    • 密文：加密算法的输出，依赖于明文与密钥，不同的密钥会产生不同的密文
    • 解密算法：加密算法的逆运算，可由 密文 + 密钥 解密

  • 密码编码系统的划分方式：包含以下三种方式

    • 将明文转换为密文的运算类型：代换（将明文中的任意元素替换为另一元素）+ 置换（将明文中的元素重新排列）
    • 所用密钥数目：对称加密（双方共享相同的密钥）+ 非对称加密（双方各自使用不同的密钥）
    • 处理明文的方式：分组密码（每次处理一个分组）+ 流密码（连续处理输入元素）

  • 密码分析：试图破解明文和密钥的过程，假设攻击者总是知道加密算法

    • 唯密文攻击：仅知道 要解密的密文；该方法强度最低，最易防范
    • 已知明文攻击：知道 要解密的密文 + 用同一密钥加密的若干明文-密文对；一般加密算法必须能经受这种攻击
      • 攻击策略：该方法依靠明密文对应关系 or 某些明文的标准化格式
    • 选择明文攻击：知道 待解密的密文 + 攻击者任意选择的明文 + 用（与待解密密文）同一密钥加密的密文
      • 攻击策略：攻击者会故意选取最有可能恢复出密钥的数据
    • 选择密文攻击：知道 待解密的密文 + 攻击者有目的选择的密文 + 用（与待解密密文）同一密钥解密的明文；该方法较少使用
    • 选择文本攻击：知道 "选择明文攻击" + "选择密文攻击" 中知道的所有信息；该方法也较少使用

  • 计算安全性：密文满足以下任一情况

    • 破译密码的代价超过密文信息的价值；代价一般难以估计，除非使用蛮力攻击
    • 破译密码的时间超过密文信息的有效生命期

    注意："蛮力攻击"指的是试遍所有可能的密钥，直到有一个合法的密钥能够把密文还原成明文

  • Feistel密码结构：所有对称加密算法（如DES）使用的最普遍的结构，每轮依据一个密钥值进行代换和置换

    • 迭代轮表达式：F 表示轮函数，子密钥\(\text{K}_i\) 由整个 K 导出

      • 加密：\(\text{L}_i \gets \text{R}_{i-1}\)，\(\text{R}_{i} \gets \text{L}_{i-1} \oplus \text{F}(\text{R}_{i-1}, \text{K}_i)\)
      • 解密：\(\text{R}_{i-1} \gets \text{L}_i\)，\(\text{L}_{i-1} \gets \text{R}_i \oplus \text{F}(\text{L}_i, \text{K}_i)\)

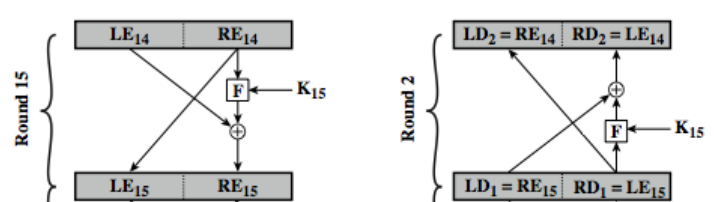
    • Feistel参数和特征：

      • 分组长度：分组越长 \(\Rightarrow\) 安全性越高，加解密速度降低；128bit 比较合理
      • 密钥长度：密钥越长 \(\Rightarrow\) 安全性越高，加解密速度降低，128bit 比较合理
      • 迭代轮数：Feistel 采用多轮加密，以取得较高的安全性；典型值是 16 轮
      • 子密钥产生算法：子密钥越复杂，密码分析越困难
      • 轮函数：轮函数越复杂，抗攻击的能力就越强
      • 快速软件加/解密：许多情况下加密算法被嵌入到应用程序中（做成硬件不方便），故算法执行速度很重要

二、数据加密标准

  • 数据加密标准(DES)：Feistel 结构的微调，同样包含 16 轮处理过程
    • 分组长度：64 bit
    • 密钥长度：56 bit；生成的 16 个子密钥 \(\text{K}_i\) 分别应用于每一轮
  • 三重DES：使用三个密钥 \(\text{K}_i\) 执行三次 DES 算法
    • 密钥长度：\(\text{K}_i\) 长度 = 56 bit \(\Rightarrow\) 有效密钥长度 = 56 bit x 3 = 168 bit，穷举攻击没有可能
      注意：联邦信息处理标准 46-3 允许仅使用两个密钥，即 \(\text{K}_1 = \text{K}_3\) \(\Rightarrow\) 有效密钥长度 = 56bit x 2 = 112 bit
    • 加密过程：\(\text{C} = \text{E}(\text{K}_3, \text{D}(\text{K}_2, \text{E}(\text{K}_1, \text{P})))\)；即 加密 \(\Rightarrow\) 解密（便于下一步使用DES加密） \(\Rightarrow\) 加密
    • 解密过程：\(\text{P} = \text{D}(\text{K}_1, \text{E}(\text{K}_2, \text{D}(\text{D}_3, \text{C})))\)；即 解密 \(\Rightarrow\) 加密 \(\Rightarrow\) 解密

三、高级加密标准

  • 高级加密标准(AES)综述：最终将取代 DES 和 3DES

    • 分组长度：128 bit
    • 密钥长度：128bit 或 196 bit 或 256 bit
    • 加密轮数：128bit 密钥 \(\Rightarrow\) 10轮；192bit 密钥 \(\Rightarrow\) 12轮；256bit 密钥 \(\Rightarrow\) 14轮

  • AES 特点：

    • 没有采用 Feistel 结构（一半修改另一半，再交换两部分），包括一个置换和三个代换

    • 输入的密钥(128bit)被扩展为44个32位字组成的数组 w[0...43]，其中第 i 轮使用 w[4i ... 4i+3] 作为该轮的轮密钥

      1. 字节代换：使用 S盒 对分组中的每个字节进行替换；S盒即"Substitution Box"
      2. 行移位：用一行代替另一行的置换
      3. 列混淆：对列的每个字节做替换，是一个与本列全部字节有关的函数
      4. 轮密钥加：利用当前分组和扩展密钥的特定部分进行按位异或，增强加密过程随机性

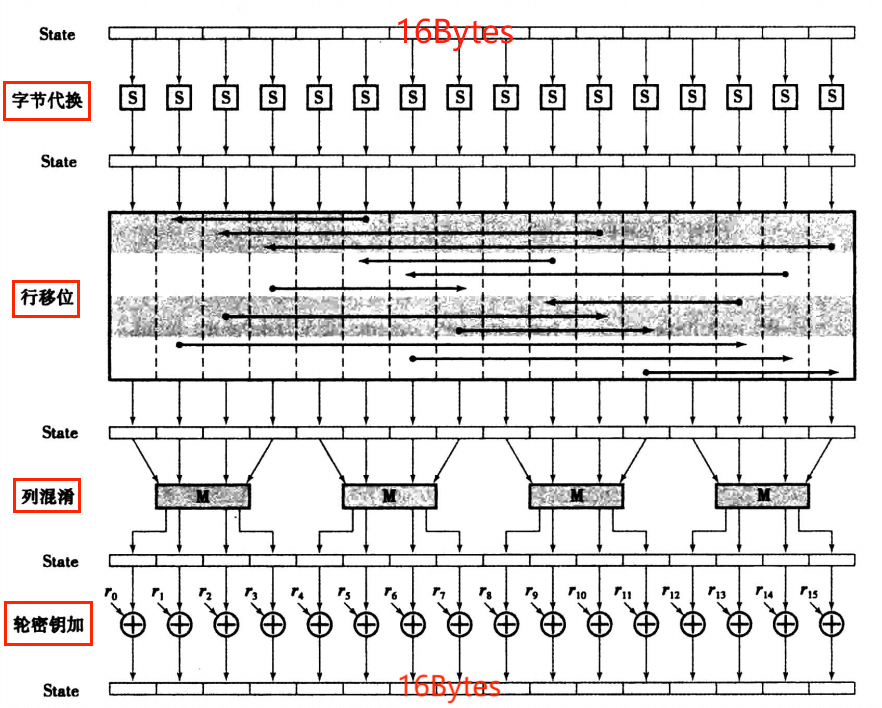
      注意：AES是面向字节操作的，在软件和硬件上都能快速地加解密，相对来说易于操作且占用存储空间少

    • 每个阶段可逆，解密过程分别为对应的逆操作

    • 加密和解密的最后一个阶段均只包含三个阶段（少了列混淆）

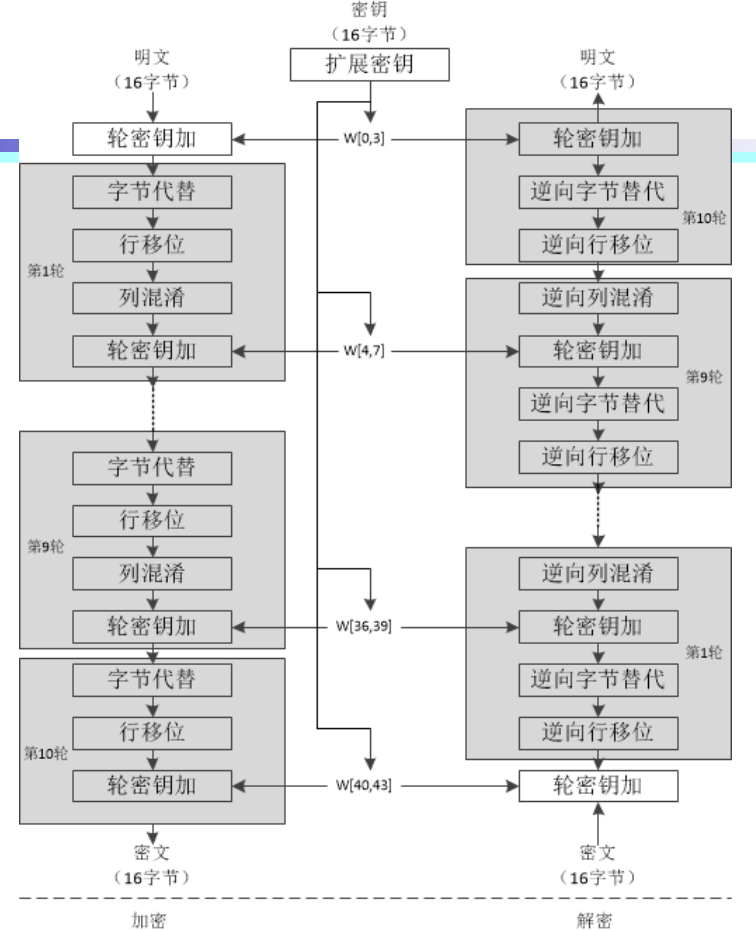
四、流密码和RC4

  • 流密码的结构：持续处理输入元素，每次加密一字节的明文

    • 伪随机字节发生器：根据输入的密钥每次随机产生一串 8bit 数字
    • 伪随机流：发生器的输出，即连续的密钥流
    • 加密流程：一个字节的明文 \(\oplus\) 一个字节的密钥流
    • 解密流程：一个字节的密文 \(\oplus\) 一个字节的密钥流

  • 流密码的用途：数据通信信道 or 网页浏览器/Web链路（不成块的数据）

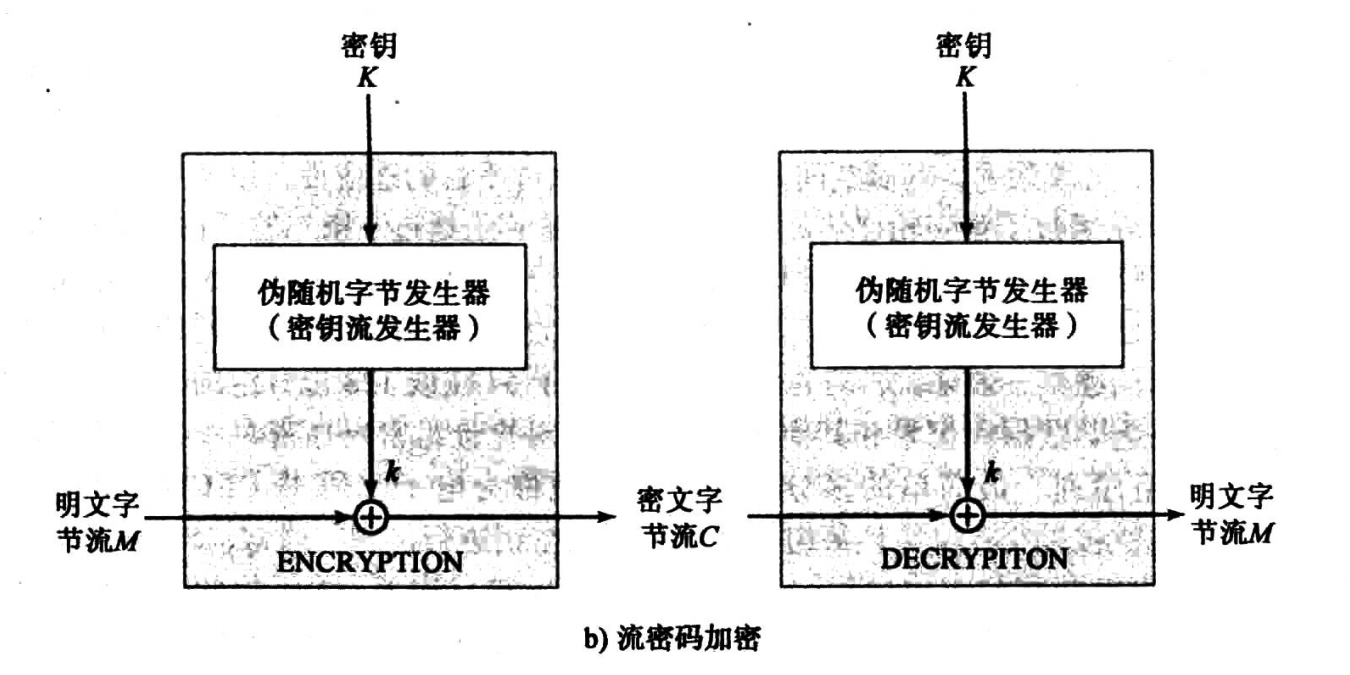
  • RC4算法：可变密码长度、面向字节操作的流密码；设状态矢量 S[0...255]，任何时刻S包含从0~255的所有 8bit 数

    1. 初始化S：先将S中各字节按升序排序，即 S[0]=0, S[1]=1, ..., S[255]=255

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      // K是变长密钥, 循环重复使用密钥K中的值赋给T
      // T是与S等长的临时矢量
      for (int i = 0; i < 255; i++) {
          s[i] = i;
          T[i] = K[i % keylen]
      }

      // 根据T对S进行初始置换, 即把S[i]与S中的另一个字节S[j]交换位置
      int j = 0;
      for (int i = 0; i < 255; i++) {
          j = (j + S[i] + T[i]) % 256;
          swap(S[i], S[j]);
      }

    2. 子密钥序列的生成：状态矢量S一旦初始化完毕，就不再使用输入密钥K

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      int i = 0, j = 0;
      // 持续生成密钥流, 故 while(1)
      while (1) {
          // S[255]完成置换后, 回到S[0]继续重复
          i = (i + 1) % 256;
          j = (j + S[i]) % 256;
          swap(S[i], S[j]);
          t = (S[i] + S[j]) % 256;
          // 加密时, 子密钥序列k与下一个明文字节异或XOR
          // 解密时, 子密钥序列k与下一个密文字节异或XOR
          k = S[t];
      }

      注意：若子密钥序列k出现了重复，密文就可能被破解；RC4应用于SSL/TLS，WEP，WPA等

五、分组密码的工作模式

  • 电子簿模式ECB：一次处理b位明文，每次加密都使用相同的密钥；任何b位明文都只有唯一的密文与之对应（类似密码簿）

    • 加密：\(\text{C}_j = \text{E}(\text{K}, \text{P}_j)\)
    • 解密：\(\text{P}_j = \text{D}(\text{K}, \text{C}_j)\)
    • 优点：有利于并行运算，误差不会传递（密文块损坏只会导致对应的明文块损坏）
    • 缺点：由于相同的明文会生成相同的密文，故同样信息多次出现可能造成泄露（借助 代换 or 重排 进行攻击）

    注意：ECB在传递 长消息 or 高度结构化的消息 时不够安全，需要能将重复的明文组加密成不同的密文组

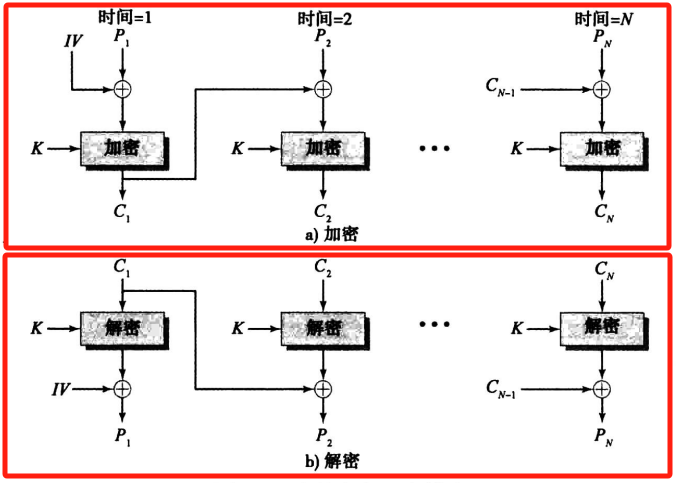
  • 密码块链接模式CBC：加密算法的每轮输入与当前明文组无固定关系（隐藏重复明文模式）；加密每一组明文使用的密钥相同

    • 加密：\(\text{C}_j = \text{E}(\text{K}, \text{C}_{j-1} \oplus \text{P}_j)\)，第一个密文块 由 第一个明文块 \(\oplus\) 随机初始向量IV 得到
    • 解密：\(\text{P}_j = \text{C}_{j-1} \oplus \text{D}(\text{K}, \text{C}_j)\)，第一个明文块 由 第一块密文解密结果 \(\oplus\) 初始向量IV 得到
    • 优点：不容易被主动攻击，安全性好于ECB；适合传输长报文
    • 缺点：不利于并行计算（序列加密），误差会传递（一个密文块\(\text{C}_j\)损坏 \(\Rightarrow\) 两个明文块\(\text{P}_j\)和\(\text{P}_{j+1}\)损坏）

  • 密码反馈模式CFB：上一轮加密结果与作为伪随机数算法的输入，而输出与明文异或送入下一层

    • 加密：\(\text{C}_j = \text{P}_{j} \oplus \text{S}_s(\text{E}(\text{K}, \text{IV}))\)，其中 \(\text{S}_s\) 表示选择加密输出的高s位
    • 解密：\(\text{P}_j = \text{C}_j \oplus \text{S}_s(\text{E}(\text{K}, \text{IV}))\)，注意解密过程使用的也是加密函数E
    • 优点：隐藏了明文模式，可将任意分组密码转化为流密码；可以及时加密传送小分组数据
    • 缺点：不利于并行处理（序列加密），误差会传递，对于不同的消息IV必须唯一

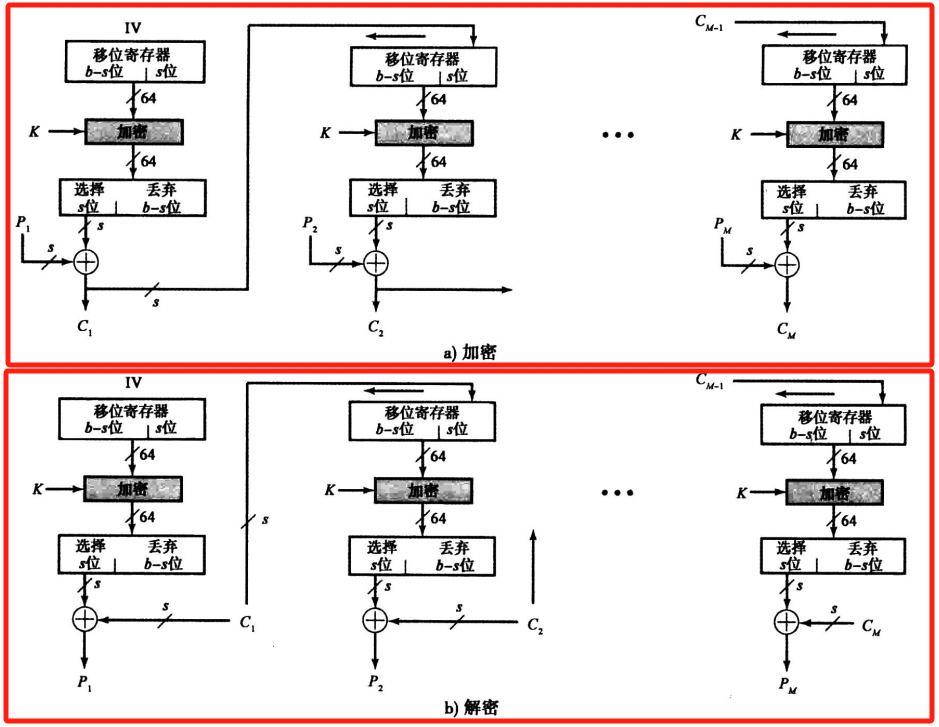
    注意：伪随机数使用移位寄存器，每轮加密左移s位，并将s位的密文填入移位寄存器的低s位置

  • 输出反馈模式OFB：与上一个CFB基本相同，同样需要初始向量IV

    • 特点：可将任意分组密码转化为流密码，且误差不会传递

    注意：相较于CFB，OFB加密算法的输入是上一轮加密算法的输出（而不是伪随机数算法的输出）

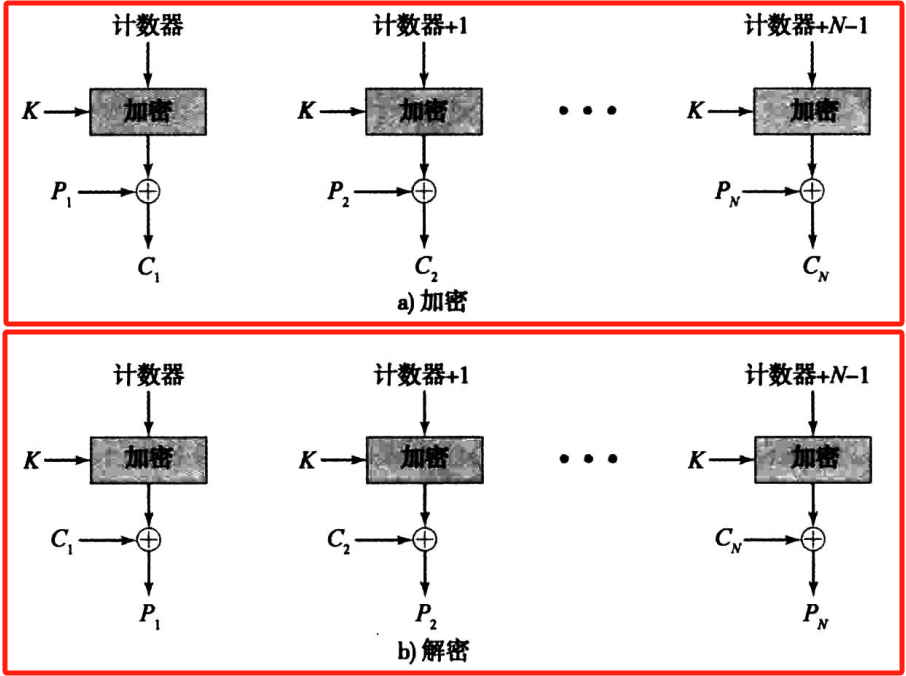
  • 计数器模式：将循环计数器的值作为加密（解密）算法的输入；在异步传输模式ATM和IPSec中应用广泛

    • 加密：\(\text{C}_j = \text{P}_j \oplus \text{E}(\text{K}, \text{cnt})\)
    • 解密：\(\text{P}_j = \text{C}_j \oplus \text{E}(\text{K}, \text{cnt})\)
    • 优点：支持并行处理，硬件效率和软件效率高
    • 缺点：若计数器的值出现重复，就有可能被攻破

六、对称加密设备的位置

  • 链路加密：在通信链路的两端设置加密设备

    • 优点：保证链路上的所有信息传输是安全的
    • 缺点：在分组交换的时候需要将消息解密成明文，此时易于受到攻击

  • 端对端加密：加密过程在主机or终端进行

    • 优点：可保证用户数据的安全
    • 缺点：如果对整个包加密，转发方就无法读取信息头，限制了路由

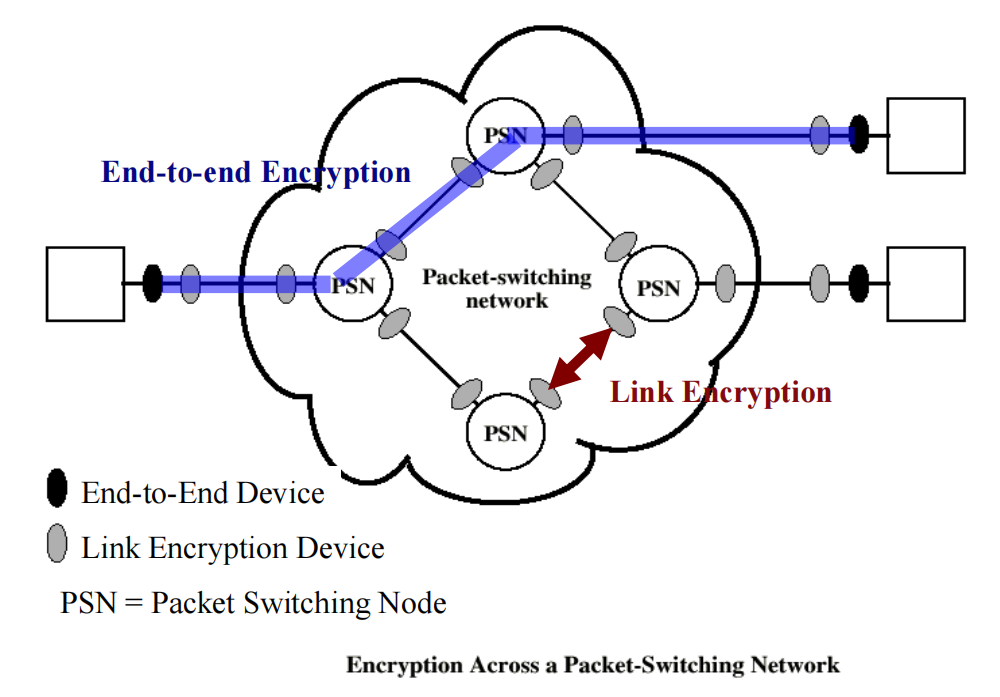
    注意：整个分组使用链路加密（路由自由），而其中的用户数据使用端对端加密（保证数据安全）

cyber security
#symmetric encryption #DES #AES
『cyber security-1』encryption algorithm
http://larry0454.github.io/2024/03/12/cyber_security/encryption-algorithm/
Author
WangLe
Posted on
March 12, 2024
Licensed under