『compiler-8』LR

LR 语法分析器

一、自底向上的语法分析

• “自顶向下”和“自底向上”的区别：

  自顶向下：从文法的开始符号出发，反复使用产生式，寻找匹配的“推导”；如递归下降语法分析，LL(1)语法分析

  自底向上：从输入串开始逐步规约，到达文法的开始符号的“规约”；如LR语法分析

  ---

• 规约：自底向上语法分析过程，即为串\(\omega\)“规约”为文法的开始符号的过程

  每个规约步骤，一个与某产生式体相匹配的特定子串被替换为该产生式头部的非终结符号

  注意：一次规约即为一次最右推导的逆操作

• 句柄：设\(S \overset{*}{\underset{rm}{\Rightarrow}} \alpha A \omega \underset{rm}{\Rightarrow} \alpha \beta \omega\)，那么紧跟在A之后的产生式\(A \rightarrow \beta\)就是串\(\alpha \beta \omega\)的一个句柄（简称\(\beta\)是一个句柄）

  注意：句柄\(\beta\)右侧的串\(\omega\)只由终结符号组成（即句子）

• 句柄剪枝：设串\(\omega\)是文法G中的句子，关于其最右推导为\(S \underset{rm}{\Rightarrow} \gamma_1 \underset{rm}{\Rightarrow} ... \underset{rm}{\Rightarrow} \gamma_{n-1} \underset{rm}{\Rightarrow} \gamma_n = \omega\)，将该推导过程反向即可获得规约过程

  每一步规约从\(\gamma_i\)中寻找句柄\(\beta_i\)，将\(A \rightarrow \beta_i\)替换入\(\gamma_i\)获得\(\gamma_{i-1}\)

• 移入——规约语法分析：维护栈保存文法符号，从左到右扫描输入串

  • 移入：将输入串的最左端转移到栈顶

  • 规约：将栈顶的文法符号串进行规约

    注意：可被规约的符号串必然在栈顶，一旦栈顶出现可被规约的串就要寻找对应的句柄进行“规约”操作

  • 接受：宣布自底向上的语法分析结束（栈中只有S，且输入已空）

  • 报错：发现一个语法错误，并调用一个错误恢复函数

• 移入——规约中的冲突：

  • 面对含有二义性的文法，由于只向前看一步，可能不确定是要执行“移入”还是“规约”
  • 找到句柄后，不确定要使用哪一个产生式进行替换规约

---

二、LR语法分析技术

• LR(k)语法的定义：目前最流行的自底向上的语法分析器⭐

  "L"表示对输入串从左到右扫描

  "R"表示构造一个最右推导序列

  "k"表示决定向前看k个输入符号，一般k=0或1

• LR(1)的特点：

  • 几乎可围绕所有的程序设计语言（只要能写出上下文无关文法）构造LR语法分析
  • 运用最通用的无回溯-规约分析技术
  • LR技术可在从左到右进行扫描时尽可能早地检测到错误
  • 可用LL语法分析的语言都可以使用LR语法分析

  ---

• 文法G的一个LR(0)项：G的一个产生式再插入一个位于它的产生式体中的某处的点

  产生式\(A \rightarrow XYZ\)可产生四个项（产生式体中可在四个位置插入点）

  产生式\(A \rightarrow \epsilon\)只能产生一个项\(A \rightarrow \cdot\)

  注意：一个项通常可以表示为一对整数：产生式编号 + 点的位置

• 项集：项的列表

• 项与语法分析：项中的定点表示目前识别到的产生式中的位置

  项\(A \rightarrow X \cdot YZ\)表示刚在输入串中看到一个可由X推导得到的串，并希望接下来能看到一个能从YZ推导得到的串

  项\(A \rightarrow XYZ \cdot\)表示已经看到了该产生式体XYZ，可将其规约为A

  ---

• LR(0)自动机

  • 增广文法：设S是文法G的开始符号

    G的增广文法G'就是在G中增加新的开始符号S'和产生式\(S' \rightarrow S\)

  • 项集的闭包CLOSURE函数：设I是文法G的一个项集，那么称CLOSURE(I)是I的一个项集：

    1. 先将I中所有的项加入到CLOSURE(I)中
    2. 若\(A \rightarrow \alpha \cdot B \beta\)在CLOSURE(I)中，则对于所有产生式\(B \rightarrow \gamma\)，项\(B \rightarrow \cdot \gamma\) 也应属于CLOSURE(I)

    反复执行上面的第二步直至CLOSURE(I)不再扩大为止

    注意：构造闭包的过程中需要时刻注意CLOSURE内的产生式体中点右侧可扩展的非终结符

    ---

  • GOTO函数：设I是一个项集，X是一个文法符号

    GOTO(I, X) = CLOSURE(J)

    其中项集J = \(\{所有形如A \rightarrow \alpha X \cdot \beta的项 | A \rightarrow \alpha \cdot X \beta \in I\}\)（即把点挪到X后面）

    注意：求解GOTO(I, X)即是将点向右挪动并求闭包的过程，蕴含了识别过程的推进

  • 规范LR(0)项集族：LR(0)自动机中的每个状态代表规范LR(0)项集族C中的一个项集，设增广文法为G'：

  void items(G’) {
  	/* 自动机的开始状态即为CLOSURE({S’ -> .S}) */
  	C = { CLOSURE({S’ -> .S}) };
  	do {
  		for (C中的每个项集I) {
  			for (每个文法符号X) {
  				if (GOTO(I, X)非空 && GOTO(I, X)不在C中) {
  					将GOTO(I, X)加入到C中;
  					/* 根据 当前项集 和 可能的输入符号 确定待加入的项集 */
  					/* GOTO -> 右移 + 扩展闭包 */
  				}
  			}
  		}
  	} while (在该轮循环中/* 有新的项集 */被加入到项集族C中);
  }

  

  LR(0)自动机示例（灰色部分都可以省略不写）

---

• LR语法分析算法

  • 文法符号与状态：若存在状态转移GOTO(\(I_i\), X) = \(I_j\)，则状态j对应了唯一的文法符号X

  • LR语法分析器：输入、输出、状态栈、分析表（ACTION + GOTO）、语法分析表

    

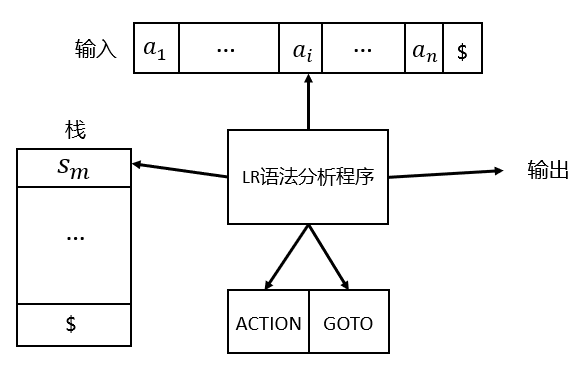
    LR语法分析器

  • LR语法分析表：由语法分析动作函数ACTION和转换函数GOTO组成

    • ACTION[i, a]：接收状态i和终结符号a（可以是$），包含以下四种动作：
      • 移入状态j：将终结符号a对应的状态压栈
      • 规约\(A \rightarrow \beta\)：将栈顶的\(\beta\)规约为其产生式头A
      • 接受：语法分析器接受输入并完成语法分析
      • 报错：在输入中发现了一个错误并执行错误恢复程序
    • GOTO[\(I_i\), A] = \(I_j\)：转移函数将状态i和非终结符号A映射到状态j，状态可以还原为其对应字符

  • LR语法分析器的格局（configuration）：栈和余下的输入

    • 格局：有序对 \((s_0s_1...s_m, a_ia_{i+1}...a_n \$)\)

    • 格局对应的最右句型：\(X_1X_2...X_ma_ia_{i+1}...a_n\)

      其中\(X_i\)是状态\(s_i\)对应的文法符号，\(s_0\)不代表任何文法符号

  • 构造SLR语法分析表（ACTION + GOTO）：基于LR(0)自动机确定语义动作，设增广文法为G'

    1. 构造G'的规范LR(0)项集族 \(C = \{I_0, I_1, ..., I_n\}\)
    2. 根据\(I_i\)构造状态i，及其语法分析动作：
       • 若 \(A \rightarrow \alpha \cdot a\beta \in I_i\) （存在移进项）并且GOTO(\(I_i\), a) = \(I_j\)（状态i在a上存在转换），则ACTION[i, a] = “移入状态j”
       • 若 \(A \rightarrow \alpha \cdot \in I_i\)且 \(A \ne S'\)（存在规约项），则对于FOLLOW(A)中的所有a，ACTION[i, a] = “规约\(A \rightarrow \alpha\)”
       • 若 \(S' \rightarrow S \cdot \in I_i\)，则ACTION[i, $] = “接受”
    3. 将未定义的ACTION条目设置为“报错”
    4. 设置语法分析器的初始状态是根据\(S' \rightarrow \cdot S\)所在项集构造得到的状态

  • LR语法分析器的行为解析：先读入当前输入符号\(a_i\)和栈顶状态\(s_m\)，再查ACTION表项：

    • 若ACTION(\(s_m\), \(a_i\)) = “移入状态s”，则格局转为\((s_0s_1...s_ms, a_{i+1}...a_n \$)\)

    • 若ACTION(\(s_m\), \(a_i\)) = “规约\(A \rightarrow \beta\)”，则格局转为\((s_0s_1...s_{m-r}s, a_ia_{i+1}...a_n \$)\)

      其中r是\(\beta\)的长度，且s = GOTO(\(s_{m-r}\), A)，输入符号保持不变

    • ACTION(\(s_m\), \(a_i\)) = “接受”，则语法分析完成

    • ACTION(\(s_m\), \(a_i\)) = “报错”，则调用错误恢复程序

  • LR语法分析算法流程：设栈内初始为\(s_0\)，输入缓冲区为输入串\(\omega\)

  初始化：字符a为ω中的/* 第一个符号 */;
  while (true) {
  	s = stack.top();
  	if (ACTION(s, a) == “移入t”) {
  		stack.push(t);
  		a = next();
  	} else if (ACTION(s, a) == “规约A -> β”) {
  		/* 先从栈中弹出β长度个状态 */
  		int cnt = |β|;
  		while (cnt > 0) {
  			stack.pop();
  			cnt--;
  		}
  		t = stack.top();
  		/* 再将产生式的头压栈 */
  		stack.push(GOTO(t, /* A */));
  		(输出产生式A -> β);
  	} else if (ACTION(s, a) == “接受”) {
  		/* 语法分析完成，跳出循环 */
  		break;
  	} else {
  		/* 调用错误恢复程序 */
  		error();
  	}
  }

---

三、更强大的LR语法分析器

• 移入——规约冲突：对于ACTION中的同一表项，既可将其设置为“移入”、又可将其设置为“规约”

  注意：移入——规约冲突产生的原因在于SLR语法分析不够强大，不能记录足够多的上下文信息，以至于无法解析部分文法

• 规范LR(1)项：对规范LR(0)项的扩展，\([A \rightarrow \alpha \cdot \beta, a]\)，其中第二分量a表示向前看符号
  规约项 \([A \rightarrow \alpha \cdot, a]\) 表示当栈顶为状态\(\alpha\)且后续符号为a时才进行“规约\(A \rightarrow \alpha\)”

• 构造CLOSURE：若要规约为A，则要先规约为B；设增广文法为G'

SetOfItems CLOSURE(I) {
	do {
		for (项集I中的每个项[A -> α.Bβ, a]) {
			for (G’中的每个产生式 B -> γ) {
				/* 能够被规约为B的串后接βa */
				for (FIRSt(βa)中的每个终结符号b) {
					将[B -> .γ, b]加入到项集I中;
				}
			}
		}
	} while (在该轮循环中有/* 新的项 */加入到I中);
    return I;
}

• 构造GOTO：描述LR(1)状态机的状态转移

SetOfItems GOTO(I) {
	J = 空集;
	for (项集I中的每个项 [A -> α.Xβ, a]) {
		/* 将点右移 */
		将项[A -> αX.β, a]加入到项集J中;
	}
	return CLOSURE(J);
}

• 构造LR(1)项集族：LR(1)自动机中的每个状态代表规范LR(1)项集族C中的一个项集，设增广文法为G'：

void items(G’) {
	/* 自动机的开始状态即为CLOSURE({S’ -> .S, $}) */
	C = { CLOSURE({[S’ -> .S, $]}) };
	do {
		for (项集族C中的每个项集) {
			for (每个文法符号X) {
				if (GOTO(I, X)非空 && GOTO(I, X)不在C中) {
					将GOTO(I, X)加入到项集族C中;
					/* 根据 当前项集 和 可能的输入符号 确定待加入的项集 */
					/* GOTO -> 右移 + 扩展闭包 */
				}
			}
		}
	} while (在该轮循环中有/* 新的项集 */加入到项集族C中);
}

---

• 构造规范LR(1)语法分析表（ACTION + GOTO）：基于LR(1)自动机确定语义动作，设增广文法为G'

  1. 构造G'的LR(1)项集族 \(C' = \{I_0, I_1, ..., I_n\}\)
  2. 根据项集\(I_i\)构造状态i，及其语法分析动作：
     • 若 \([A \rightarrow \alpha \cdot a \beta, b] \in I_i\)（存在移进项），且GOTO(\(I_i\), a) = \(I_j\)，则ACTION[i, a] = “移入状态j”
     • 若 \([A \rightarrow \alpha \cdot, a] \in I_i\) 且 \(A \ne S'\)（存在规约项），则ACTION[i, a] = “规约 \(A \rightarrow \alpha\)”
     • 若 \([S' \rightarrow S \cdot, \$] \in I_i\)，则ACTION[i, $] = “接受”
  3. 未定义的ACTION条目都设置为“报错”
  4. 设置语法分析器的初始状态为包含 \([S' \rightarrow \cdot S, \$]\) 的项集构造得到的状态

• LR语法中的错误恢复

  • 恐慌模式：设出错部分可由某个非终结符号A推导出，一旦出错：
    1. 从栈顶向下扫描直至找到状态s，且这个状态s拥有一个在A上的转换GOTO(s, A)
    2. 跳过若干个输入符号，直至发现一个可以合法地跟在非终结符号A后面的符号
    3. 将GOTO(s, A)压栈

  注意：这种恢复方法试图装作完成了对非终结符号A的解析，并继续前进

• 短语层次修复：根据LR(1)语法分析表中的报错条目推断语法错误的类型，修改栈顶状态或当前第一个输入符号