『compiler-7』optimization
代码优化
一、基本块与流图
基本块:一段顺序执行的代码块,满足以下三条性质:
- 基本块中的代码是连续的语句序列
- 程序的执行只能从基本块的第一条语句进入
- 程序的执行只能从基本块的最后一条语句离开
注意:每条中间代码属于且仅属于一个基本块
流图:节点是基本块、有向边表示基本块之间的前驱后继关系(转移、条件假转移、紧随块)
基本块划分算法:输入中间代码语句序列,输出基本块序列
确定入口语句:
- 整个语句序列的第一条语句是入口语句
- 由转移(有条件or无条件)语句转移到的首条语句属于入口语句
- 紧跟在跳转语句之后的首条语句属于入口语句
注意:第二种表示基本块的起点、第三种表示基本块的出口
确定基本块内容:入口语句直到下一条入口语句(or结束语句)之间的所有语句属于同一个基本块
基本块内优化:消除局部公共子表达式、窥孔优化
DAG图表示:DAG图是有向无环图
- 叶节点:由变量名or常量值所标记
- 中间节点:由中间代码中的操作符所标记
消除局部公共子表达式:输入基本块内的中间代码序列,输出删除局部公共子表达式的DAG
- 建立空节点表,该表条目记录了变量名(常量值)+ 节点序号([x, i])
- 从第一条中间代码开始,构建DAG:注意每一步用于分配的节点新编号都从“1”开始递增分配
- 设 z = x op y,x的节点编号为i(y同理),查找节点表:
- 若找得到,先记下x的节点编号i(y同理,用于下一步找op)
- 若找不到,在DAG中新建叶节点(标记为x),在节点表中增加新表项 (x, i),y同理
- 在DAG中寻找中间节点op,满足其左操作数编号为i,右操作数编号为j
- 若找得到,先记下op的节点编号k(用于下一步更新z的编号)
- 若找不到,设其编号为k,并在DAG中新建子树x-z-y,即把z的左右节点分别连接x和y
- 在节点表中寻找z:
- 若找得到,将z对应的节点编号更改为k
- 若找不到,在节点表中增加新表项(z, k)
- 设 z = x op y,x的节点编号为i(y同理),查找节点表:
- 对所有中间代码重复上述操作步骤
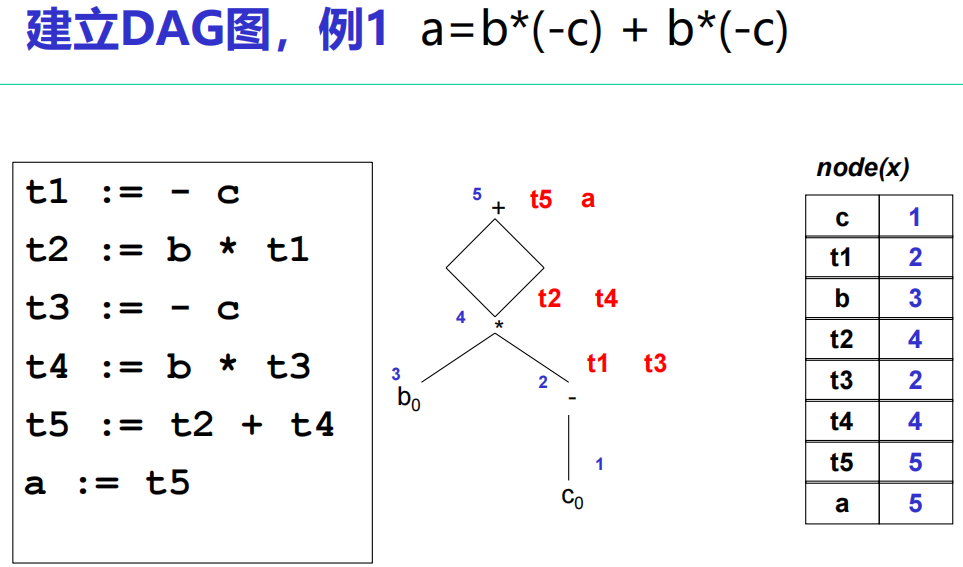
注意:在 z = x op y 中, x 和 y 均可为空;若 op 为空,则 z 的编号由 x(或 y)赋值
从DAG图重新导出中间代码:输入DAG,输出中间代码序列
- 初始化放置DAG图的中间节点的空栈
- 若DAG中所有中间节点都已进入栈,则直接转入最终步骤v.
- 否则,选取一个尚未进入节点栈,但其所有父节点都已进入节点栈的中间节点n,将其推入栈
或者 选择没有父节点的中间节点n,将其推入栈 - 沿着n的最左子节点链,将符合iii.中条件的中间节点推入栈,直到不满足iii.条件就重新转入ii.
- 最后,将节点栈中的各中间节点依次弹出,整理成中间代码序列
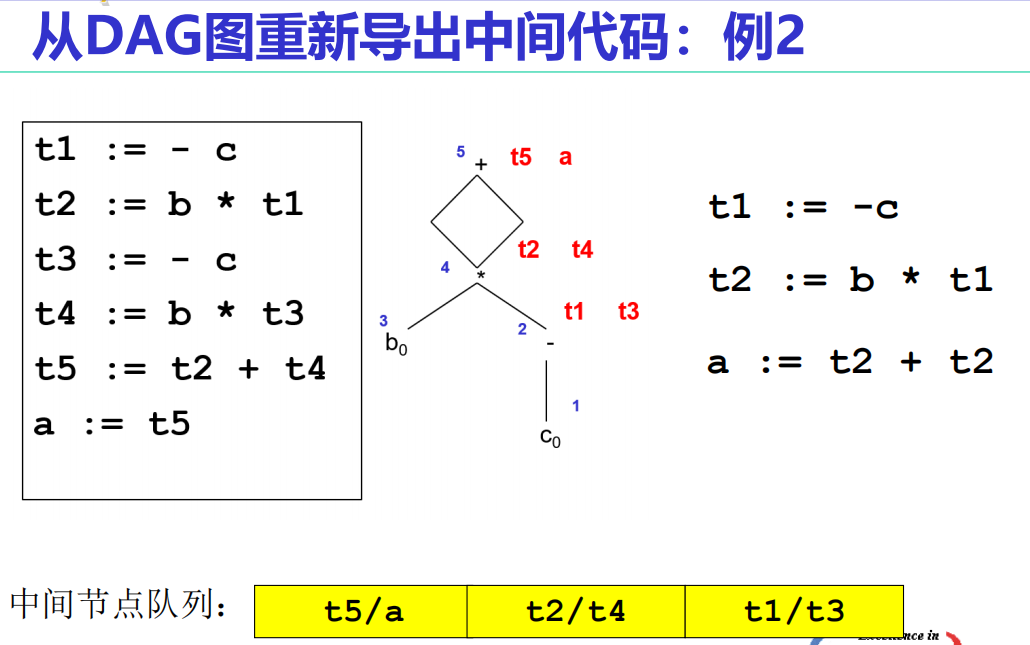
op节点实际应被看作 存储运算结果 的中间节点
窥孔优化:“窥孔”指仅关注目标指令的一个较短序列;“优化”指删除(or 改进)其中的部分代码
常数合并和常量传播:
- 常数合并:将能够在编译时计算出值的表达式用相应的值替代,如 A = 2 + 3 + C \(\Rightarrow\) A = 5 + C
- 常量传播:在编译时已知的变量值代替程序中对这些变量的引用
二、全局优化
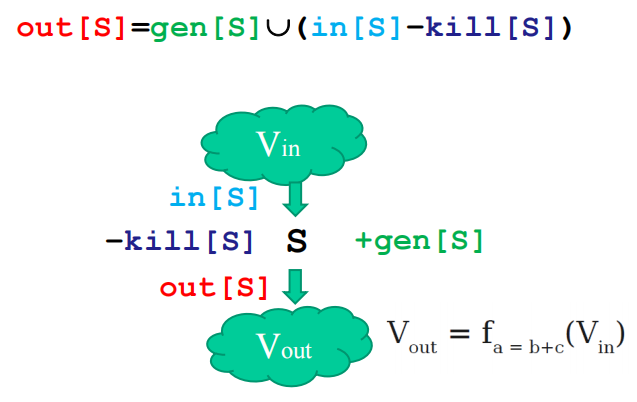
数据流方程:out[S] = gen[S] \(\cup\) (in[S] - kill[S])
- out[S]:表示在S末尾得到的数据流信息
- gen[S]:表示在S本身产生的数据流信息
- in[S]:表示进入S时的数据流信息
- kill[S]:表示S注销的数据流信息
到达定义的数据流分析:分析某个变量的值是在哪里被定义的;自前向后计算
设基本块中的某条定义语句为 d1: u := v op w,则由数据流方程为 out[d1] = gen[d1] \(\cup\) (in[d1] - kill[d1])
- gen[d1] = { d1 },表示 d1 语句产生了一个定义点
- kill[d1]:包含整个程序中其它所有对 u 定义的定义语句的集合
基本块B的数据流方程:out[B] = gen[B] \(\cup\) (in[B] - kill[B])
kill[B] = kill[d1] \(\cup\) ... \(\cup\) kill[dn]
gen[B] = gen[dn] \(\cup\) (gen[d(n-1)] - kill[dn]) \(\cup\) ... \(\cup\) (gen[d1] - kill[d2] - ... - kill[dn])
in[B] = \(\bigcup_{\text{B的所有**前驱**基本块P}}\text{out[P]}\)
out[B]:直接由数据流方程导出
到达定义数据流分析:输入程序流图、各基本块的kill与gen集合;输出各基本块的in和out集合
- 将所有基本块的out集合初始化为\(\varnothing\)
- 根据in[B]和out[B]的公式,先后计算(更新)各基本块的in与out集合
注意:若某个基本块的 out 发生了改变,则要重新求解其所有后继块的 in 集合 - 若某一轮更新迭代中存在out[B]发生了变化,则循环迭代ii. 直至所有out[B]都不再变化
活跃变量分析:分析变量x在程序的某个点(及其之后的任意执行路径)是否被使用(活跃);自后向前计算
基本块B的数据流方程:in[B] = use[B] \(\cup\) (out[B] - def[B])
def[B]:基本块B中的,定义先于任何对其使用的变量集合
use[B]:基本块B中的,使用先于任何对它的定义的变量集合
out[B] = \(\bigcup_{\text{B的所有**后继**基本块P}}\text{in[P]}\)
in[B]:直接由数据流方程导出
活跃变量数据流分析:输入程序流图、各基本块的use与def集合;输出各基本块的in和out集合
- 将所有基本块的in集合初始化为空集
- 根据out[B]和in[B]的计算公式,先后计算(更新)各基本块的out与in集合
注意:若某个基本块的 in 发生了改变,则要重新求解其所有前驱块的 out 集合 - 若某一轮更新迭代中存在in[B]发生了变化,则循环迭代ii. 直至所有in[B]都不再变化