『database-4』relational data theory
关系数据理论
一、函数依赖
函数依赖的定义:设 R(U) 是属性全集 U 上的关系模式,X、Y \(\subseteq\) U,r $$ R,t、s \(\in\) r
若 t[X] = s[X],则有 t[Y] = t[Y],称为 X 函数决定 Y,或 Y 函数依赖于 X,记作 X \(\rightarrow\) Y
注意:X \(\rightarrow\) Y 可以表述为对于属性组X上的任一值,Y中有唯一的值与其对应平凡与非平凡的函数依赖:设 X \(\rightarrow\) Y
- 平凡的函数依赖:若 Y \(\subseteq\) X,则称 X \(\rightarrow\) Y 是平凡的函数依赖;任一关系模式下平凡依赖总是成立
- 非平凡的函数依赖:若 Y \(\nsubseteq\) X,则称 X \(\rightarrow\) Y 是非平凡的函数依赖
决定因素:设 X \(\rightarrow\) Y,则称 X 为决定因素
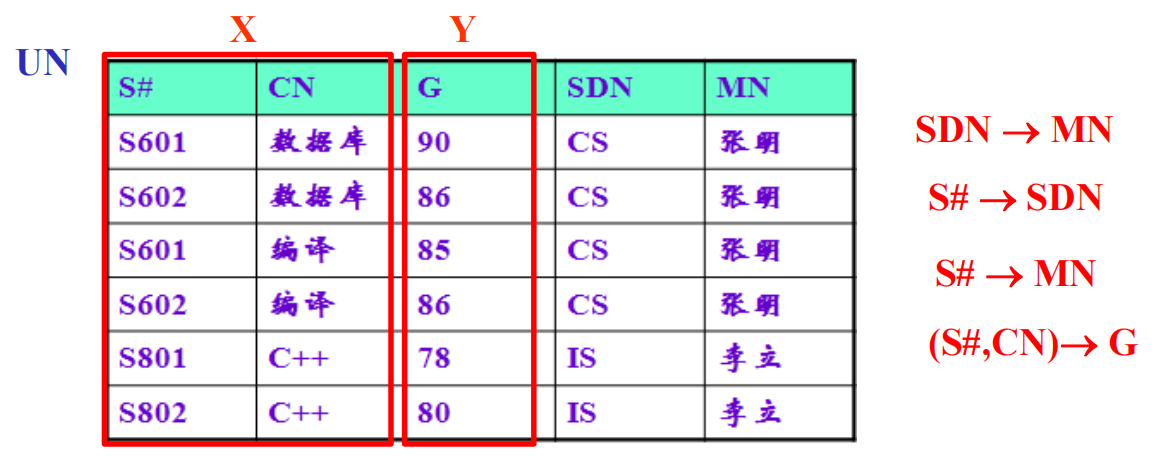
从 X 到 Y 满足单射 注意:函数依赖不随时间而变;虽然关系 R 随时间而变化,但 X \(\rightarrow\) Y 总保持不变
函数依赖与属性间联系:可分为 1 : 1、1 : n、n : m 三种
- 一对一:若 X 与 Y 满足一对一关系(学号 与 身份证号),则有 X \(\leftrightarrow\) Y
- 一对多:若 X 与 Y 满足一对多关系(部门号 与 部门员工号),则有且仅有 Y \(\rightarrow\) X
- 多对多:若 X 与 Y 满足多对多关系(学号 与 课程号),则 X 与 Y 之间不存在函数依赖
注意:函数依赖是根据具体场景下的语义确定的
函数依赖类型:设关系模式 R(U) 下有 X \(\rightarrow\) Y
- 完全函数依赖:若对 X 的任意真子集 X',都有 X' \(\nrightarrow\) Y,则 Y 对 X 完全函数依赖,记作 X \(\xrightarrow{f}\) Y
- 部分函数依赖:若不满足完全函数依赖,则为部分函数依赖,记作 X \(\xrightarrow{p}\) Y
- 传递函数依赖:若 X \(\rightarrow\) Y、Y \(\rightarrow\) Z,但 Y \(\nrightarrow\) X,则称 Z 对 X 传递函数依赖,记作 X \(\xrightarrow{t}\) Z 注意:这里若 Y \(\rightarrow\) X,相当于 X 与 Y 之间满足一对一关系,故有 X \(\xrightarrow{直接}\) Z,而不是间接依赖
候选码:设 K 为 R<U, F> 中的属性组,若 K \(\xrightarrow{f}\) U,则称 K 是 R 的候选码(主码是其中一个候选码)
注意:“完全依赖”表明码具有最小性,若抽去任意一个属性该候选码将失去唯一标识性主属性与非主属性:
- 主属性:包含在任意一个候选码中的属性
- 非主属性:不包含在任何码中的属性
逻辑蕴含:设关系模式为 R<U, F>,若可从 F 中的函数依赖推导出 X \(\rightarrow\) Y,则称 F 逻辑蕴含 X \(\rightarrow\) Y
函数依赖集F的闭包:为 F 所逻辑蕴含的函数依赖的全体称作F的闭包,记作 \(\text{F}^+\)
Armstrong公理系统:设关系模式为 R<U, F>
- 自反律:若 Y \(\subseteq\) X,则 X \(\rightarrow\) Y 为 F 所蕴含(平凡依赖)
- 增广律:若 X \(\rightarrow\) Y 被 F 所蕴含,则 XZ \(\rightarrow\) YZ 被 F 所蕴含(可拼接相同的属性组)
- 传递律:若 X \(\rightarrow\) Y 和 Y \(\rightarrow\) Z 为 F 所蕴含,则 X \(\rightarrow\) Z 为 F 所蕴含(注意这不是传递依赖)
Armstrong公理系统推论:
合并规则:设 X \(\rightarrow\) Y,X \(\rightarrow\) Z,有 X \(\rightarrow\) YZ(直接用定义证明)
伪传递规则:设 X \(\rightarrow\) Y、WY \(\rightarrow\) Z,有 WX \(\rightarrow\) Z(增广律WX \(\rightarrow\) WY + 传递律)
分解规则:设 X \(\rightarrow\) Y,若 Z \(\subseteq\) Y,有 X \(\rightarrow\) Z(自反律Y \(\rightarrow\) Z + 传递律)
合并规则 + 分解规则:X \(\rightarrow\) \(A_1A_2\dots A_k\) 成立 \(\Leftrightarrow\) X \(\rightarrow A_i\) 成立(i = 1, 2, ..., k)
依赖集的闭包:设关系模式为 R<U, F>,为 F 所逻辑蕴含的函数依赖的全体称作 F 的闭包,记作 \(\text{F}^+\)
属性集X关于依赖集F的闭包:设关系模式 R<U, F>,且 X \(\subseteq\) U
\(X_F^+ = \{A \text{ | } X \rightarrow A \text{ 能由F根据Armstrong公理推导出}\}\)(可理解为X所能决定的属性集合)如何求解 \(X_F^+\) ?利用以下算法反复迭代(计算不动点)

注意:迭代中的每一步,是抽取闭包集合中的一个属性子集A,查找是否存在由以该子集为决定因素的函数依赖
定理:X \(\rightarrow\) Y 能够由 F 根据 Armstrong 公理导出 \(\Leftrightarrow\) Y \(\subseteq\) \(\text{X}_F^+\)
Armstrong公理系统的有效性与完备性:
- 有效性:由 F 出发根据 Armstrong 公理推导出的每个函数依赖必定在 F 所蕴含的函数依赖的全体中
- 完备性:F 所蕴含的函数依赖全体为 \(\text{F}^+\) 中的每个函数依赖,必可由F根据Armstrong公理导出
函数依赖集等价:设函数依赖集F、G,若\(\text{F}^+ = \text{G}^+\),则称 F 与 G 等价;\(\text{F}^+ = \text{G}^+ \Leftrightarrow \text{F} \subseteq \text{G}^+\) 且 \(\text{G} \subseteq \text{F}^+\)
极小依赖集:若 F 同时满足下列条件,则称 F 为一个极小函数依赖集
- 依赖右部A必须是单属性:F 中的任一函数依赖 X \(\rightarrow\) A,A 必须是单属性的
- 不存在多余的函数依赖 X \(\rightarrow\) A:F 中不存在函数依赖 X \(\rightarrow\) A,使得 F 与 F - {X \(\rightarrow\) A} 等价
- 依赖左部无多余属性Z:F 中不存在函数依赖 X \(\rightarrow\) A,使得 Z \(\subset\) A,F 与 F - {X \(\rightarrow\) A} \(\cup\) {Z \(\rightarrow\) A} 等价
依赖集的极小化算法:每个函数依赖集 F 均等价于一个极小依赖集 \(\text{F}_m\)
- 对 F 中的所有依赖 X \(\rightarrow\) \(A_1A_2\dots A_n\),直接用 X \(\rightarrow\) \(A_k\)(k = 1, ..., n)替代它(右部单属性化)
- 对 F 中的所有依赖X \(\rightarrow\)
A,设X = \(B_1B_2\dots B_n\),若A \(\in\) \((X -
B_i)_F^+\),则X = X - \(B_i\)(消去左部多余属性)
注意:这一步 不需要 更改依赖集合 F - 对 F 中的所有依赖 X \(\rightarrow\) A,令 G = F - {X \(\rightarrow\) A},若 A \(\in\) \((X)_G^+\),则从F中去掉 X \(\rightarrow\) A(消去多余依赖)
二、规范化
范式的等级:1NF \(\supset\) 2NF \(\supset\) 3NF \(\supset\) BCNF \(\supset\) 4NF \(\supset\) 5NF;低级关系模式可以分解为若干高一级的关系模式
1NF:关系表中每一行和列的交叉位置上总是一个单一的值(而非值的集合),即不允许“表中套表”
2NF:R \(\in\) 1NF,且 每个非主属性完全依赖于所有候选码
- 1NF \(\rightarrow\) 2NF:将不完全依赖于码的非主属性A分离出来,与其依赖的主属性搭配起来形成新的2NF模式
3NF:R \(\in\) 2NF(非主属性不部分依赖于任何候选码),且 每个非主属性都不传递依赖于的任何候选码
- 2NF \(\rightarrow\) 3NF:将传递路径上的各决定因素分离出来作为新的码,切断原先的传递路径
BCNF:设关系模式 R<U, F>,若 F 中的每个决定因素都包含了候选码,则 R \(\in\) BCNF
注意:根据上述定义,BCNF 也可以定义为:不存在主属性和非主属性,部分依赖or传递依赖于任何候选码- 所有非主属性都完全函数依赖于每个候选码
- 所有主属性都完全函数依赖于每个不包含它的候选码
- 没有任何属性完全函数依赖于非码的任何一组属性
注意:若决定因素仅包含候选码的一部分,则存在对候选码的部分依赖
若决定因素不包含候选码,则存在对候选码的传递依赖
三、多值依赖与第四范式
多值依赖的定义:设关系模式为 R(U),X、Y、Z \(\subseteq\) U,且 Z = U - X - Y(Z 与 X和Y均互不相容)
给定(X, Z)下的任一值(x, z),有一组 Y 的值 \(\{y \text{ | } y \in \text{Dom(Y)}\}\),使得该组Y值仅取决于x值而与z值无关
记作 X \(\rightarrow \rightarrow\) Y
注意:多值依赖反映了属性之间 1 : n 的关系,常出现在同一组织下客体间双向全选的情景中关系中存在多值依赖:找到X值相同的两个元组,仅交换Y值,若两个新的元组均仍在原关系中,说明 X \(\rightarrow \rightarrow\) Y
注意:上述方法说明,只需取定X的值,就足以对Y的值集产生决定性影响平凡与非平凡的多值依赖:设 X \(\rightarrow \rightarrow\) Y,Z = U - X - Y
- 平凡多值依赖:若 Z = \(\varnothing\) ,则为平凡多值依赖(U仅由X和Y组成)
- 非平凡多值依赖:若 Z \(\ne\) \(\varnothing\),则为非平凡多值依赖(U除了X和Y,还有Z)
多值依赖的性质:设 Z = U - X - Y
- 对称性:若 X \(\rightarrow \rightarrow\) Y,则 X \(\rightarrow \rightarrow\) Z(Y 与 Z 对称)
- 传递性:若 X \(\rightarrow \rightarrow\) Y,Y \(\rightarrow \rightarrow\) Z,则 X \(\rightarrow \rightarrow\) Z - Y
- X \(\rightarrow\) Y 可以看作是 X
\(\rightarrow \rightarrow\) Y
的特殊情况 (Y值集 \(\Rightarrow\)
Y单值)
- 若 X \(\rightarrow \rightarrow\) Y,X \(\rightarrow \rightarrow\) Z,则有 X \(\rightarrow \rightarrow\) YZ
- 若 X \(\rightarrow \rightarrow\) Y,X \(\rightarrow \rightarrow\) Z,则有 X \(\rightarrow \rightarrow\) Y \(\cap\) Z
- 若 X \(\rightarrow \rightarrow\) Y,X \(\rightarrow \rightarrow\) Z,则有 X \(\rightarrow \rightarrow\) Y - Z,X \(\rightarrow \rightarrow\) Z - Y
多值依赖与函数依赖的区别:
- X \(\rightarrow \rightarrow\) Y 在
U 上成立,则必在W(XY \(\subseteq\) W
\(\subseteq\)
U)上成立,反之不一定(多值依赖与其余属性Z有关)
X \(\rightarrow\) Y 在任意属性集W(XY \(\subseteq\) W \(\subseteq\) U)上总是成立 - X \(\rightarrow\) Y 在 R(U)
上成立,则对于任意 Y' \(\subseteq\)
Y,X \(\rightarrow\) Y' 总是成立
X \(\rightarrow \rightarrow\) Y 在 R(U) 上成立,但对于任意 Y' \(\subseteq\) Y,X \(\rightarrow \rightarrow\) Y' 不一定成立
- X \(\rightarrow \rightarrow\) Y 在
U 上成立,则必在W(XY \(\subseteq\) W
\(\subseteq\)
U)上成立,反之不一定(多值依赖与其余属性Z有关)
4NF:设关系模式 R<U, F>,对于R的每个非平凡的多值依赖 X \(\rightarrow \rightarrow\) Y,X都含有码
由于“码”表示依赖具有唯一值性,故非平凡且左部含码的多值依赖本质上即为函数依赖
注意:4NF也可定义为:R \(\in\) BCNF,且不存在非平凡的非函数依赖的多值依赖规范化过程:见下图
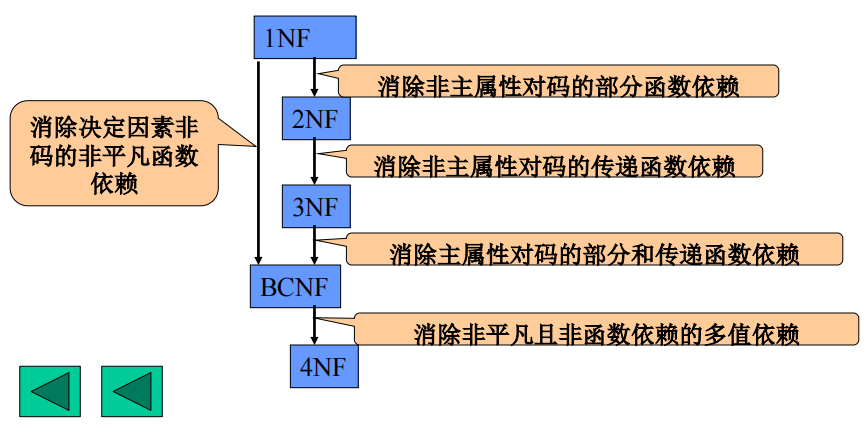
证明 (x+1)NF \(\subset\) xNF:反设 R \(\in\) (x+1)NF 且 R \(\notin\) xNF, 由 xNF 的反向性质推出 (x+1)NF 的矛盾
四、模式分解理论
关系模式分解:
- 函数依赖的投影 \(F_i\):\(F_i = \{X \rightarrow Y \text{ | }X \rightarrow Y
\in F^+ \land XY \subseteq U_i\}\),称 \(F_i\) 为 F 在 \(U_i\) 上的投影
注意:函数依赖的分集合要求依赖的左右两侧必须均在\(U_i\)中,且 X \(\rightarrow\) Y可由 F 推导 - 关系模式的分解 \(\rho\):\(\rho = \{R_1<U_1, F_1>, \dots,R_n<U_n, F_n>\}\) 其中 $_{i=1}^n U_i = $ U,且不存在 \(U_i \subseteq U_j\)(i \(\ne\) j)
- 函数依赖的投影 \(F_i\):\(F_i = \{X \rightarrow Y \text{ | }X \rightarrow Y
\in F^+ \land XY \subseteq U_i\}\),称 \(F_i\) 为 F 在 \(U_i\) 上的投影
无损分解:设 \(\rho = \{R_1<U_1, F_1>, \dots ,R_n<U_n, F_n>\}\) 是 R<U, F> 的一个分解,定义 \(m_{\rho} = \Join \Pi_{R_i}(r)\)
其中 \(\Pi_{R_i}(r)\) 为 关系 r \(\in\) R 上关于对应属性列 \(U_i\) 的投影,\(\Join \Pi_{R_i}(r)\) 表示将各分模式上的属性列连接起来
若对任意关系 r \(\in\) R,都有 r = \(m_{\rho}(r)\),则称 \(\rho\) 为无损分解无损分解的判定算法:设 \(\rho = \{R_1<U_1, F_1>, \dots,R_k<U_k, F_k>\}\),\(U = \{A_1, \dots A_n\}\)
- 建立n列k行的二维表M:列表示属性\(A_i\)、行表示一个分模式\(R_i\)
- 初始化二维表:若 \(A_j \in U_i\),则 \(m_{ij} = a_j\);若 \(A_j \notin U_i\),则 \(m_{ij} = b_{ij}\)
- 对 \(F_i\) 中的每个函数依赖
X \(\rightarrow\)
Y,若M中存在横向元组\(t_1\)、\(t_2\),使得 \(t_1[X] =
t_2[X]\),则对每个\(A_i \in Y\):
- 若 \(t_1[A_i] = t_2[A_i]\) 中有一个为 \(a_i\),则将另一个也改成 \(a_i\)
- 否则,令 \(t_1[A_i] \gets t_2[A_i]\)(二维表中\(t_1\)在\(t_2\)的上方)
- 反复迭代第3步,根据最终结果判断是否为无损分解:
- 若二维表中的某行为 \(a_1\dots a_n\),则为无损分解
- 否则,为有损分解
无损分解的充要条件:设 R<U, F> 的一个分解为 \(\rho = \{R_1<U_1, F_1>,R_2<U_2, F_2>\}\)
\(\rho\) 为无损分解 \(\Leftrightarrow\) \(R_1\) 和 \(R_2\) 的共同属性至少构成 \(R_1\)、\(R_2\) 之一的候选码,即 \(U_1 \cap U_2 \rightarrow U_1 - U_2 \in F^+\)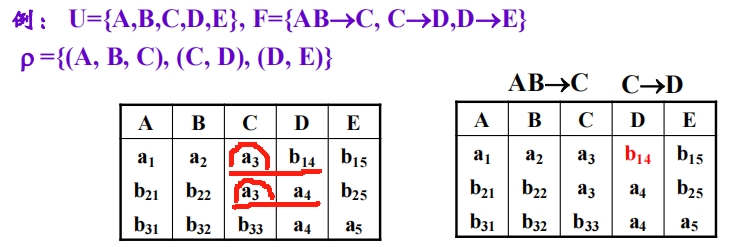
分解的保持函数依赖性:若 \(F^+ = (\bigcup_{i=1}^n F_i)^+\),则称 \(\rho\) 保持函数依赖
即 R 中的每个函数依赖都可以从 \(F_1, \dots F_n\) 的并集中逻辑导出判断是否保持函数依赖:设 \(G = \{\bigcup_{i=1}^n F_i\}\),则保持函数依赖有\(F^+ = G^+\) \(\Leftrightarrow\) \(F \subseteq G^+ \land G \subseteq F^+\)
即对任意 X \(\rightarrow\) Y \(\in\) F,若总有 Y \(\in\) \(X_{G^+}^+\),说明 X \(\rightarrow\) Y \(\in\) \(G^+\)(充要性定理),即 \(F \subseteq G^+\),反之亦然
注意:这里是在判断对于 F 中的 X \(\rightarrow\) Y,X 能否借助 \(G^+\) 决定 Y模式分解能够达到的范式等级:
- 若要求分解保持函数依赖,模式分解总可以达到3NF,但不一定能达到BCNF
- 若要求分解保持函数依赖,且保持无损连接性,模式分解可以达到3NF,但不一定能够达到BCNF
- 若要求分解具有无损连接性,模式分解一定至少能够达到4NF
达到3NF的、保持函数依赖的模式分解:(自底向上合成法)
对F进行极小化处理,并令 F \(\gets\) \(\text{F}_m\)
将不在F中的属性\(\text{U}' = \{A_1, \dots A_k\}\)剔除出来,单独构成一个关系模式\(\text{R}'\),并令 U \(\gets\) U - \(\text{U}'\)
若有 X \(\rightarrow\) A,且 XA = U,则最终分解为 \(\rho = \{\text{R}\}\),分解算法结束
对F中具有相同左部的规则分成k组,每组函数依赖所涉及的全体属性(左部 + 右部)设为\(\text{U}_i\)
若有 \(\text{U}_i \subseteq \text{U}_j\)(i \(\ne\) j,出现冗余模式),则要去掉 \(\text{U}_i\);设 \(\text{F}_i\) 是 F 在 \(\text{U}_i\) 上的投影
则 \(\rho = \{\text{R}_i <\text{U}_i, \text{F}_i> \text{ | } i = 1 \dots k \} \cup \text{R}'\) 是 R<U, F> 的保持函数依赖的分解,且均有 $_i $ 3NF
达到3NF的、同时保持无损连接与函数依赖的分解:
设\(\rho\)是R<U, F>上的依据合成法分解得到的已经保持函数依赖的3NF分解,X是R的码
若有某个分\(\text{U}_i\),X \(\subseteq \text{U}_i\),则 \(\rho\) 为所求
否则,令\(\tau = \rho \cup \{\text{R}^*<\text{X}, \text{F}_X>\}\),\(\tau\) 即为所求分解(\(\text{F}_X\) 表示F在X上的投影)
达到BCNF、具有无损连接性分解算法:(自顶向下分解法)令 \(\rho = \{\text{R}<\text{U}, \text{F}>\}\)
若 \(\rho\) 中的各关系模式均 \(\in\) BCNF,则算法结束
否则,设 \(\rho\) 中的\(\text{R}_i<\text{U}_i, \text{F}_i>\) \(\notin\) BCNF,则存在 X \(\rightarrow\) A \(\in\) \(\text{F}_i^+\),X 不是 \(\text{R}_i\) 的码;故 XA \(\subset\) \(\text{U}_i\)
对 \(\text{R}_i\) 分解为 \(\sigma = \{\text{S}_1, \text{S}_2\}\),\(\text{U}_{\text{S}_1} = \text{XA}\)(避免决定因素不含码),且 \(\text{U}_{\text{S}_2} = \text{U}_i - \{\text{A}\}\),再令 \(\text{R}_i \gets \sigma\)反复执行上一步骤,直至无法继续分解(\(\rho\) 中均为 BCNF)
五、候选码的求解理论与算法
依赖中的属性类型:可分为4类
- L类:仅出现在F的函数依赖左部的属性
- R类:仅出现在F的函数依赖右部的属性
- N类:在F的函数依赖的左右两侧均未出现过的属性
- LR类:在F的函数依赖左右两边均出现过的属性
快速求解候选码:设关系模式 R<U, F>,X(X \(\subseteq\) U)的类型分类如下
- L类属性:X必出现在R的所有候选码中
注意:若 \(\text{X}_{\text{F}}^+ = \text{U}\),则X为R的唯一候选码 - R类属性:X不出现在R的任意候选码中
- N类属性:X必出现在R的所有候选码中
注意:若 X 是N类和L类组成的属性集,且 \(\text{X}_{\text{F}}^+ = \text{U}\),则X为R的唯一候选码
- L类属性:X必出现在R的所有候选码中
函数关系依赖图:设关系模式为R<U, F>
节点:对应 U 中的单属性
有向边:<\(\text{A}_i\), \(\text{A}_j\)> 表示一个函数依赖 \(\text{A}_i \rightarrow \text{A}_j\)
原始点:仅有引出线而无引入线,对应L类属性
终结点:仅有引入线而无引出线,对应R类属性
途中点:既有引出线又有引入线,对应LR类属性
孤立点:既无引出线又无引入线,对应N类属性
关键点:原始点和孤立点统称为关键点
关键属性:关键点对应的属性
回路:类比有向图中的有向环
孤立回路:不能由其它节点到达的回路
候选码的图论判定方法:
- 若依赖图中存在关键点,则关键点对应属性必在R的所有候选码中,所有终结点必不在任何候选码中
- 属性集X是R的唯一候选码 \(\Leftrightarrow\) X可到达G中的任意节点
注意:在单属性依赖集中,R具有唯一候选码 \(\Leftrightarrow\) G中不存在独立回路 - 设 Y 是中途点,则Y必在某个候选码中 \(\Leftrightarrow\) Y为某个独立回路的节点
单属性依赖集候选码图论求解法:设 F 为单属性依赖集
- 求出F的极小依赖集\(\text{F}_m\),构造对应的函数依赖图G
- 从G中找出关键属性集X
- 若G中不存在独立回路,则X为R的唯一候选码
- 否则,从各独立回路中取一节点对应属性与X组成一个候选码(取尽所有组合)
多属性依赖集候选码图论求解法:设 F 不是单属性依赖集
- 将R的所有属性分为四类,并令X代表L、N(即关键属性),Y代表LR类
- 求 \(\text{X}_{F}^+\),若 \(\text{X}_{F}^+ = \text{U}\),即X为R的唯一候选码,候选码求解结束
- 否则,求 \((\text{XB})_{F}^+\),若
\((\text{XB})_{F}^+ = \text{U}\),则 XB
是一个候选码,候选码中属性的个数由此确定
其中B是Y中的若干个属性;迭代求解的过程要按照B中属性个数递增的顺序(1, 2, ..., n)求解