『compiler-3』parser
语法分析
一、语法分析的功能
- 根据文法规则,从源程序单词符号串中识别语法成分
- 进行语法检查、报告错误
二、自顶向下分析
- 分析过程:给定符号串s,根据文法为s构造语法树;若成功,则s为语法树对应的语法成分,即
s\(\in\) L(G[Z])
注意:该过程之前需要先预测串s属于哪种语法成分,且可能会回溯
三、二义性问题
- 文法的二义性:对于文法的某个句子,若存在两棵不同的语法树,则该文法是二义性文法
注意:具有二义性的文法,会导致句型的句柄不唯一 - 二义性文法:0~3型文法均可能产生二义性
- 优先级规定:含有低优先级运算符的推导式被置于上层规则,以消除二义性
如正则表达式的规则定义从上到下依次为 选择、连接、重复
四、左递归问题
左递归文法的定义:存在形如 \(\text{U} \rightarrow \text{U} \dots\) 的规则,其中 \(\text{U} \in \text{V}_n\)
注意:左递归文法无法使用自顶向下的方法进行分析,需要消除左递归消除左递归的三条规则
规则一:设 \(\text{U} \rightarrow \text{xy | xw | ... | xz}\),可将其替换为 \(\text{U} \rightarrow \text{x(y | w | ... | z)}\),即提公因子x
规则二:设 \(\text{U} \rightarrow \text{x | y | ... | z | Uv}\),可将其替换为 \(\text{U} \rightarrow (\text{x | y | ... | z})\{\text{v}\}\)
规则三:设 \(\text{P} \rightarrow \text{Pv | a}\),可将其替换为 \(\text{P} \rightarrow \text{aP'} \text{且 P'} \rightarrow \text{vP' | }\epsilon\),即改成右递归
注意:后两条规则都表示后接任意个串v的句子
消除间接左递归:
将文法各规则重新排列,使得后续规则产生式体中的非终结符仅来自其前规则的产生式头
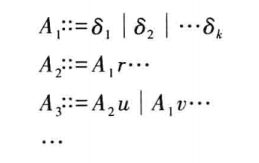
根据以下算法消除左递归
\[ \begin{array}{ll} \mathbf{for} \text{ i} \gets 1 \text{ to } n \\ \qquad \mathbf{for } \text{ j} \gets 1 \text{ to } i-1 \\ \qquad \qquad \text{将形如 }A_i \rightarrow A_j r\text{ 的单独产生式替换为} \\ \qquad \qquad A_i \rightarrow \delta_1 r | \cdots | \delta_k r\text{,}其中A_j \rightarrow \delta_1 | \cdots | \delta_k ,即把\text{ }A_j\textbf{ 代入}\text{ }A_i \\ \qquad \qquad 其余产生式保持不变 \\ \qquad \text{消除 }A_i \text{ 中的直接左递归} \end{array} \]
注意:各非终结符的排列顺序不同,最后获得的文法在形式上也是不一样的,但各文法间是等价的
五、回溯问题
- 有关回溯:自顶向下语法分析中可能出现的问题
- 造成回溯的条件:文法中某个非终结符号的规则右部有多个产生式体,选择错误可能导致回溯
如 \(\text{U} \rightarrow \alpha_1 \text{ | } \alpha_2 \text{ | ... | }\alpha_n\),不确定要选择哪个产生式体进行推导 - 回溯的问题:需要重新分析,严重降低效率
- 造成回溯的条件:文法中某个非终结符号的规则右部有多个产生式体,选择错误可能导致回溯
- FIRST集合:设产生式体为 \(\alpha_i\),则 \(\text{FIRST(}\alpha_i\text{)} = \{a \text{ | }
\alpha_i \overset{*}{\Rightarrow}a\dots, \text{ } a \in
\text{V}_t\}\),即\(\alpha_i\)所可能推出的句子的首单词集
注意:为了避免回溯,需要有 \(\text{FIRST(}\alpha_i\text{)} \cap \text{FIRST(}\alpha_j\text{)} = \varnothing\)(i \(\ne\) j),即需要有确定的产生式选择 - 避免回溯:上述避免回溯的条件无法避免时采取的措施
- 对原文法反复提取左因子,直至满足避免回溯的条件
- 超前扫描(偷看):向前多预读几个字符
- 如何实现不带回溯的自顶向下的语法分析?
- 文法不是左递归的
- 满足 \(\text{FIRST(}\alpha_i\text{)} \cap \text{FIRST(}\alpha_j\text{)} = \varnothing\)(i \(\ne\) j)
六、递归下降的语法分析
实现方法:为文法中的每个非终结符编写一个分析程序;根据当前输入符号调用正确的分析程序
调用约定:
- 进入某个非终结符的分析程序时,当前语法成分的首字符已被读入
- 分析程序结束前,需要预读下一个单词,以保证当前子程序退出时,已经预读好了下一个单词
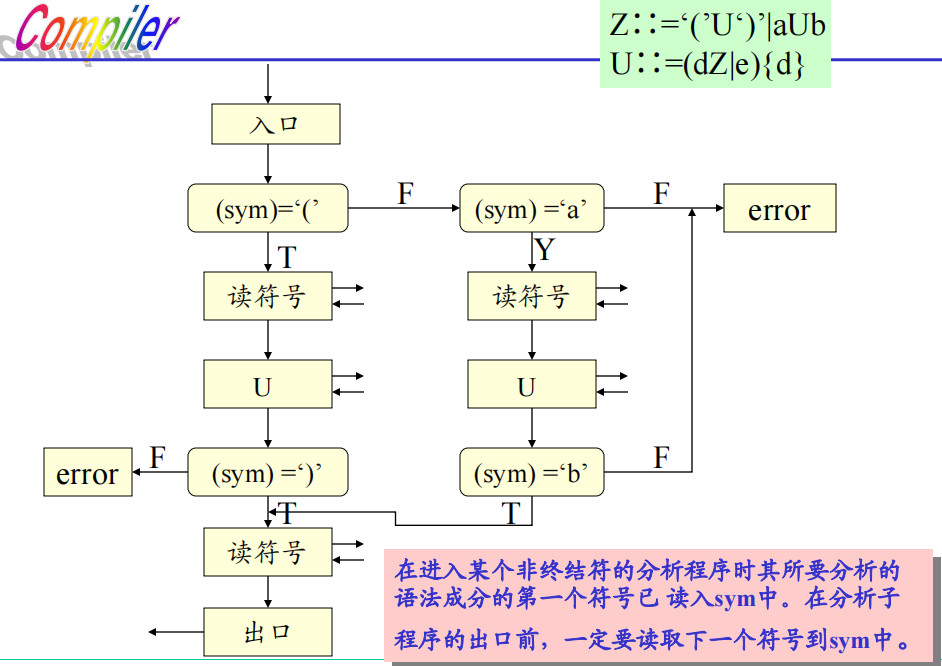
非终结符Z的分析流程 注意:递归下降语法分析是最左推导的过程
七、LL(1)语法分析
FIRST集与FOLLOW集
FIRST集:FIRST(\(\alpha\)) = \(\{a \text{ | } \alpha \overset{*}{\Rightarrow} a\dots, a \in V_t\}\),表示串\(\alpha\)可以推出的任意符号串的第一个终结符
注意:若\(\alpha \overset{*}{\Rightarrow} \epsilon\),则 $\(FIRST(\)\(),即FIRST集中可能包含\)$FIRST集合的构造方式:设X为某个文法符号
若 \(X \in V_t\),则 FIRST(X) = \(\{\text{X}\}\),终结符本身的 FIRST 集合即是自己
若 \(X \in\) \(V_n\),且 \(X \rightarrow a \alpha\)(\(a \in V_t\)),则 \(a \in\) FIRST(\(X\))
若 \(X \rightarrow \epsilon\),则 \(\epsilon \in\) FIRST(\(X\))若\(X \in V_n\),则对于X的产生式\(X \rightarrow Y_1Y_2\dots Y_k\)
- 先把FIRST(\(Y_1\)) - \(\{\epsilon\}\) 加入到 FIRST(\(X\))中
- 若 \(\epsilon \in\) FIRST(\(Y_1\))、FIRST(\(Y_2\))、...、FIRST(\(Y_{i-1}\))(i \(\ge\) 2),即 \(Y_1\dots Y_{i-1} \overset{*}{\Rightarrow}
\epsilon\)
则将 FIRST(\(Y_i\)) - \(\{\epsilon\}\) 加入到 FIRST(\(X\)) 中;否则不会继续向 FIRST(\(X\)) 中添加符号
注意:若最终 \(\epsilon \in\) FIRST(\(Y_1\))、...、FIRST(\(Y_k\)),则 \(\epsilon \in\) FIRST(X) - 若\(X \rightarrow \epsilon\),则有 \(\epsilon \in\) FIRST(\(X\))
X是符号串 \(X_1X_2\dots X_n\):根据以上三种情形求解任意符号串的FIRST集合
- 先把FIRST(\(X_1\)) - \(\{\epsilon\}\) 加入到FIRST(\(X\))中
- 若 $$ FIRST(\(X_1\))、FIRST(\(X_2\))、...、FIRST(\(X_{i-1}\))(i \(\ge\) 2)
则将 FIRST(\(X_i\)) - \(\{\epsilon\}\) 加入到 FIRST(X) 中;否则不会继续向 FIRST(X) 中添加符号
注意:若最终 $$ FIRST(\(X_1\))、...、FIRST(\(X_k\)),则 $$ FIRST(X) - 若 \(X = \epsilon\),则 FIRST(\(X\)) = \(\{\epsilon\}\)
FOLLOW集:FOLLOW(A) = \(\{a \text{ | } Z \overset{*}{\Rightarrow} \dots Aa \dots, a \in V_t, A \in V_n\}\),其中 Z 是文法的开始符号
FOLLOW集的构造方式:设#表示输入右端的结束符号
- 初始操作:先将#加入到 FOLLOW(Z) 中
- 迭代操作:直至所有非终结符的FOLLOW集都不再变化
- 若\(A \rightarrow \alpha B \beta\),则将 FIRST(\(\beta\)) - \(\{\epsilon\}\) 加入到 FOLLOW(B) 中
- 若 \(A \rightarrow \alpha B\),或 \(A \rightarrow \alpha B \beta\) 且 \(\beta \overset{*}{\Rightarrow} \epsilon\),则将 FOLLOW(A) 加入到 FOLLOW(B) 中
注意:FIRST集合可以有\(\epsilon\);FOLLOW集合中不能有\(\epsilon\)(确定的终结符才能决定产生式选择),但可以有#
LL(1)文法:从左向右 + 最左推导 + 向前看k = 1个符号
- LL(1)文法的充要条件:无二义性 + 无左递归 +
消除回溯;设 \(A \rightarrow \alpha \text{ | }
\beta\)
- FIRST(\(\alpha\)) \(\cap\) FIRST(\(\beta\)) = \(\varnothing\)
- 若 \(\beta \overset{*}{\Rightarrow}
\epsilon\),则FIRST(\(\alpha\))
\(\cap\) FOLLOW(A) = \(\varnothing\),对 \(\alpha\) 同理
注意:由LL分析表的构造方法可知,若上式两者有交集,对于同一输入符号会产生选择冲突
- LL(1)文法的充要条件:无二义性 + 无左递归 +
消除回溯;设 \(A \rightarrow \alpha \text{ | }
\beta\)
LL分析法:从左向右扫描、执行最左推导
LL分析程序的组成部分:分析表(A, a) + 总控程序 + 符号栈
- 分析表(A, a):一格表项只能填两种类值:
- M[A, a] = \(A \rightarrow \alpha_i\),表示用A匹配输入串中的当前字符a
- M[A, a] = error,表示无法用A匹配输入串中的当前符号a
- 符号栈:存放终结符和非终结符(栈底为#),维护当前推导过程中的信息
- 分析表(A, a):一格表项只能填两种类值:
分析表的构造方法:设 \(A \rightarrow \alpha\)为文法中的任一规则,a为终结符或$
- 对于 FIRST(\(\alpha\))
中的每个终结符a,将 \(A \rightarrow
\alpha\) 写入M[A, a]
注意:\(\alpha\)的首终结符确定了唯一的产生式选择 - 若 \(\alpha \overset{*}{\Rightarrow}
\epsilon\),则对于 FOLLOW(A) 中的任意符号b,将\(A \rightarrow \epsilon\) 写入M[A, b]
注意:此时A后紧跟的终结符确定了唯一的产生式选择 - 将剩余未填写的分析表格标记为error
注意:对于二义性or左递归的文法,至少有一个M表项填有多条规则
- 对于 FIRST(\(\alpha\))
中的每个终结符a,将 \(A \rightarrow
\alpha\) 写入M[A, a]
执行程序:
- 初始操作:先将#和开始符号Z依次推入符号栈
- 迭代操作:设当前栈顶符号为X,输入终结符为a
- 若 X = a = #,则分析成功,即栈和输入序列均只剩 #
- 若 X = a \(\ne\) #,则匹配成功,将X弹出栈,并读入下一个输入符号
- 若 X \(\in V_n\),查分析表 M:
- M[X, a] = \(X \rightarrow
\text{UVW}\),则先将X弹出栈,并将WVU依次压入栈
注意:要将U暴露在栈顶,符合最左推导 - M[X, a] = \(X \rightarrow \epsilon\),则只将X弹出栈(不必将\(\epsilon\)压栈,因为将\(\epsilon\)压栈后又弹栈)
- M[X, a] = error,则转入错误处理程序
- M[X, a] = \(X \rightarrow
\text{UVW}\),则先将X弹出栈,并将WVU依次压入栈