『database-1』relational database

关系数据库

一、关系的数学定义

• 域：一组具有相同数据类型的值的集合，如整数、实数、布尔值等

• 元组和分量：设一组域为 \(D_1\), ..., \(D_n\)，这些域中可存在相同的
  这些域的笛卡尔积为 \(D_1 \times \dots \times D_n = \{(d_1, \dots d_n) | d_i \in D_i, i = 1, \dots n\}\)

  • 元组：\(D_1 \times \dots \times D_n\)中的一个元素 \((d_1, \dots d_n)\) 为一个元组
  • 分量：n元组中的每一个值 \(d_i\) 称为分量

• 笛卡尔积与二维表：表头代表各个域 \(D_i\)，表头下方每一行是一个元组

• 基数：一个域允许的不同取值的个数；\(D_1 \times \dots \times D_n\) 的基数为 \(\prod_{i=1}^n m_i\)，其中 \(m_i\) 是域 \(D_i\) 的基数

  ---

• 关系：笛卡尔积 \(D_1 \times \dots \times D_n\) 的子集称为各域上的关系，记作 \(R(D_1, \dots, D_n)\)，表示 n 元关系

• 关系与二维表：表头由各个 \(D_i\) 组成；每一列对应一个域，并附加一个属性名，将该列作为属性
  注意：每一列必须拥有不同的属性名；属性 \(A_i\) 的取值范围为 \(D_i\)，称为值域

• 关系的性质：

  • 各列是同质的，即每一列的分量来自同一个域
  • 行的顺序无所谓，可以调换；列的顺序也无所谓，可以调换
  • 每一分量必须是不可再分的数据，这被称为满足第一范式（1NF）
  • 任意两个元组不能完全相同；不同的列可以出自同一个域

  注意：由于集合中不能包含重复元素，关系的任意两个元组不可完全相同，做投影运算后也必须对行去重

---

二、关系数据模型

• 关系模型的数据结构：实体间的联系均采用单一的数据结构“关系”表示0

  • 码（key）：又被称作键

    • 候选码：可唯一标识一个元组，且具有最小性（不关心多余的属性）的属性组
    • 主码（码）：选定关系中其中一个候选码为主码

  • 主属性：主码中的各属性称为主属性

  • 非主属性：不包含在任何候选码中的属性

    ---

  • 关系模式：关系的描述，表示为 R(U, D, dom, F)

    • R：表示关系名
    • U：表示组成该关系的属性名的集合
    • D：表示 U 中属性所来自的域
    • dom：表示属性向域的映像集合
    • F：表示属性间依赖关系的集合

    关系模式可以简记为 R(\(A_1\), ..., \(A_n\))，其中R为关系名、\(A_i\) 为属性名

    注意：关系模式是相对稳定的；关系则是动态的，可随时间变化

  • 关系数据库的“型”和“值”：

    • 型：关系模式的集合；关系模式可以理解为数据库逻辑设计的“类型”（schema）
    • 值：关系的集合；关系可以看作给定时刻数据模式中数据的一个“快照”（instance）

  ---

• 关系模型的语义约束

  • 实体完整性：若属性组A是关系R的主属性，则属性组A中的各属性均不能取空值（不存在 or 不完整）

  • 参照完整性：描述关系之间属性的相互引用：设R是参照关系、S是被参照关系

    • 外部码：设F是关系R的一个 or 一组属性，但不是R的码 若F与关系S的主码Ks定义在同一个域，则称F为R的外部码（而不是本关系的主码）
    • 参照完整性：若R的外部码F 与 S的主码P相对应 则R中的任意元组的F中的各属性值或 等于S中某个元组的P值，或者全取空值

    注意：由于P是关系S的主码，P可以取遍所有合法值，故关系R中的非空F必须取自S中某个元组的P值

  • 用户定义完整性：用户针对具体的应用环境定义的完整性约束条件

• 关系模型的数据操作：以关系运算为基础，操作的对象和结果都是集合

  • 关系代数：通过代数方式操纵数据
  • 关系演算：其中包括元组关系演算 + 域关系演算，通过逻辑方式操纵数据

  ---

• 关系模型的优点和缺点：

  • 优点：
    1. 建立在严格的数学基础上
    2. 使用单一的概念（关系）描述
    3. 数据结构简单直观、易于理解
    4. 存取路径对用户透明，数据独立性高，简化了DB开发工作
  • 缺点：
    1. 由于存取路径对用户透明，查询效率不如层次模型与网状模型
    2. 提高性能需要查询优化，增加DBMS的开发难度

---

三、关系代数

• 关系代数的分类：

  • 基本关系代数：并、差、广义笛卡尔积、选择、投影

  • 扩展关系代数：交、连接、除法

• 常规集合运算：二元运算，两个关系必须是同类关系（度相同、对应属性值需来自同一个域）
  设 R 和 S 分别表示两个同类关系，其度分别为 n 和 m，其分别包含 \(k_1\) 和 \(k_2\) 个元组：

  • 并：\(R \cup S = \{t | t \in R \lor t \in S\}\)，即将两个关系的所有元组合并成新的关系
  • 交：\(R \cap S = \{t|t \in R \land t \in S\}\)，即将两个关系的相同元组组建成新的关系
  • 差：\(R - S = \{t | t \in R \land t \notin S\}\)，即属于R但不属于S的元组构成的新的关系
  • 广义笛卡尔积：\(R \times S = \{(r, s)\text{ | }r \in R \land s \in S\}\)，即将R中各元组和S中各元组拼接为新的元组
    注意：\(R \times S\) 的度为 n + m（即拼接两个关系的各属性）；\(R \times S\) 中共包含 \(k_1 \times k_2\) 个元组
    \(R \times S\) 中的元组的前 n 个分量来自 R 中的元组，后 m 个分量来自 S 中的元组

• 特有关系运算：

  • 选取：\(\sigma_F(R) = \{t|t \in R, F(t)=\text{true}\}\)，即将关系R中符合条件 F 的元组筛选出来
    其中 F 是选择条件，基本形式为 \(x\theta y\)，x 和 y表示属性名或常数、\(\theta\) 表示算数 or 逻辑运算符

  • 投影：\(\Pi_A(R) = \{t[A] \text{ }| \text{ }t \in R, A \subseteq U\}\)，即从关系R(U)中抽取若干属性列 并 删去重复行 其中 A 是若干属性名构成的集合，指向各待选列（元组的分量）

    注意：“选择”是从行的角度做筛选，“投影”是从列的角度做筛选

    ---

  • \(\theta\) 连接：\(R \underset{X \theta Y}{\Join} S = \{(r, s) \text{ | }r \in R \land s \in S \land r[X] \text{ } \theta \text{ }s[Y]\}\)，即从\(R \times S\)中选择满足 \(\theta\) 的元组对
    \(r[X] \text{ } \theta \text{ } s[Y] = \text{true} \Leftrightarrow\) 元组r在属性组X上的取值 与 元组s在属性组Y上的取值满足比较关系 \(\theta\)
    注意：\(\theta\) 连接中不要求属性组X和Y相同，只需可比较就行；自然连接要求属性组X和Y必须相同

  • 自然连接：\(R \Join S = \{(r, s)[U-X] \text{ | } r \in R \land s \in S \land r[X] = s[X]\}\)，其中U为R和S的全体属性集合
    注意：自然连接是比较属性组同名，且最终去除重复公共列的等值连接

  • 计算连接：找出R和S中分别在X和Y上满足 \(\theta\) 关系的元组对，将这些元组对拼接构成新的关系
    计算自然连接：找出R和S在公共属性X上等值的元组对，将这些元组对拼接 并 对列去重构成新的关系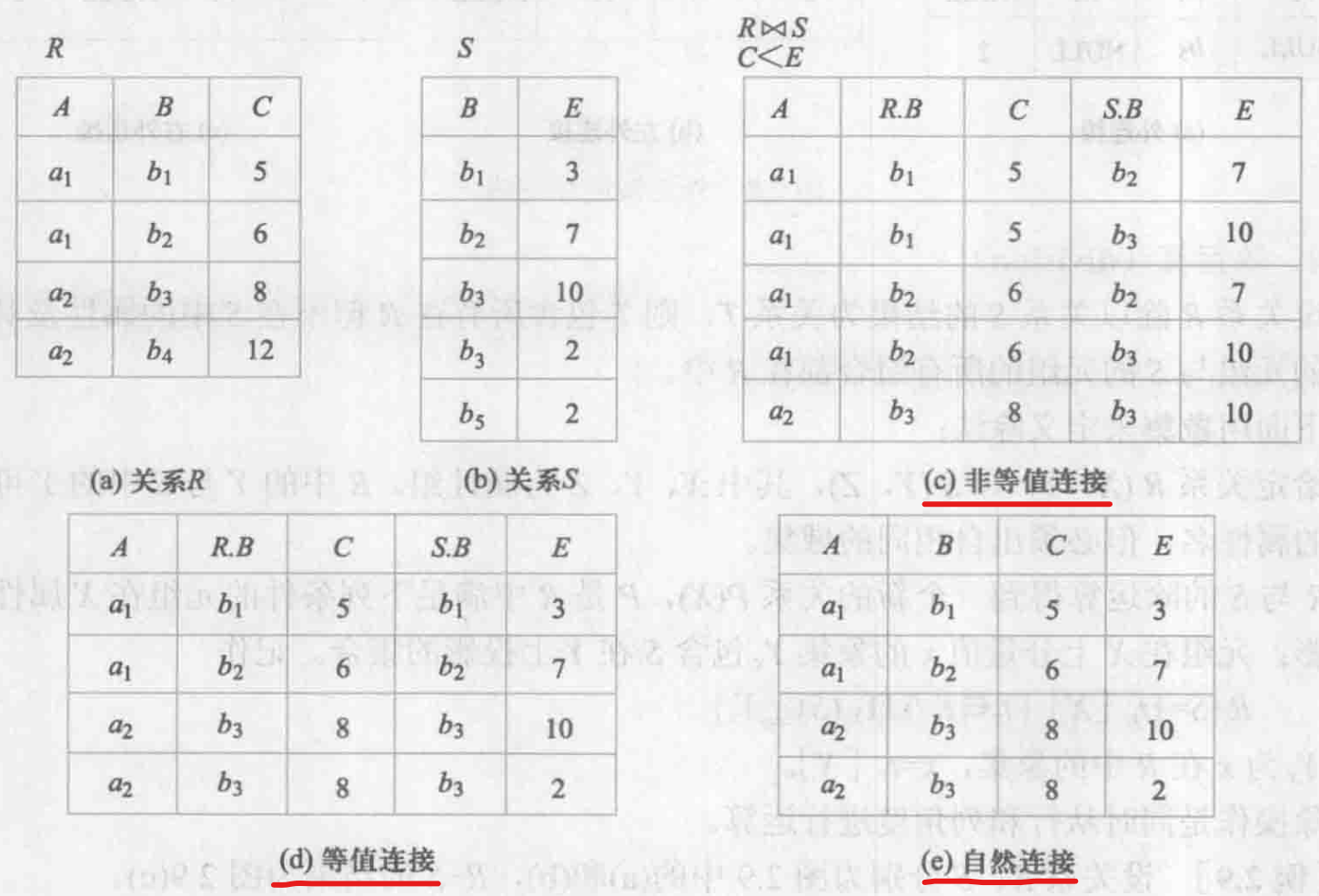

    常见的连接运算

注意：若R和S具有同名属性A，笛卡尔积或连接后应使用各自关系名修饰属性A，如R.A、S.A以做区分

---

• 除法：设R(X, Y)和S(Y, ...)，\(R➗S = \{t \text{ | } t \in \Pi_X(R) \land s \in S \land (t, s) \in R\}\)
  注意：被除关系的属性有且仅有两种：属性组X 和 属性组Y

• 计算除法：先求出\(\Pi_X(R)\)，再分别计算\(\Pi_X(R)\)中各元素的象集\(Y_x\)，找出所有满足 \(\Pi_Y(S) \subseteq Y_x\) 的X值

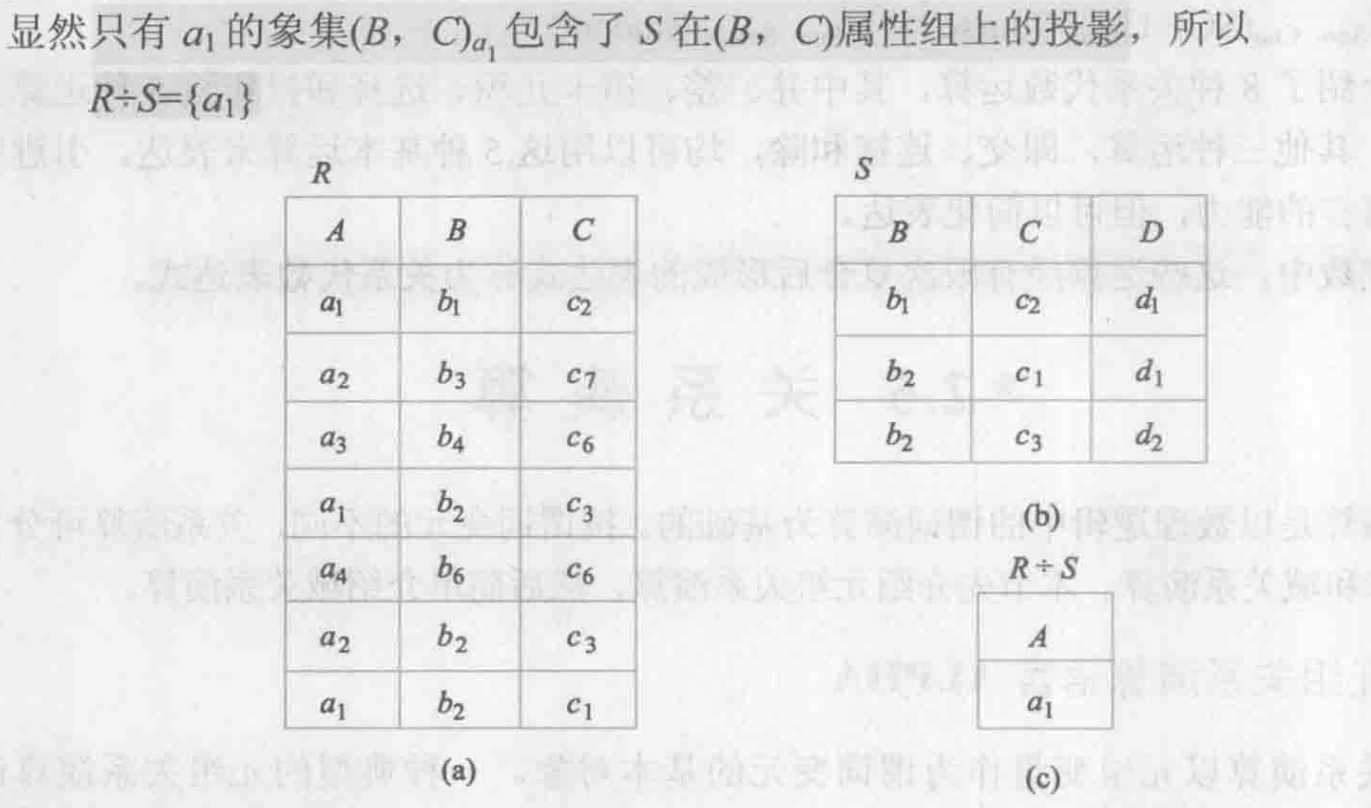
  除法运算

• 关系代数的适用场景：各运算之间常常组合使用

  • 选择：选出表中所有满足某条件的条目
  • 投影：获得表中需要的属性信息
  • 自然连接：根据已有的表一信息，借助连接属性 引入组装 表二的信息（表一信息还不够）
  • 除法：从表一中获得包含表二某属性组下全部信息的属性信息，一般先投影后做除法

---

四、关系演算

• 元组关系演算：以元组为变量

  • 元组演算表达式：\(\{t \text{ | }\Phi(t)\}\)，表示所有使谓词\(\Phi\)为真的元组集合，由原子公式 + 运算符组成
  • 原子公式：主要分为以下三类：
    1. R(t)：断言元组 t 是关系 R 中的元组
    2. t[i] \(\theta\) u[j]：断言元组 t 的第i个分量 与 元组 u 的第j个分量满足比较关系\(\theta\)
    3. t[i] \(\theta\) c 或 c \(\theta\) t[i]：断言元组 t 的第i个分量 和 常量 c 满足比较关系\(\theta\)
  • 元组演算公式的递归定义：
    1. 每个原子公式是公式
    2. 若 \(\Phi\) 是公式，则 \(\forall t(\Phi)\)、\(\exist t(\Phi)\) 都是公式，其中t是约束元组变量
    3. 若\(\Phi_1\)和\(\Phi_2\)都是公式，则\(\Phi_1 \land \Phi_2\)、\(\Phi_1 \lor \Phi_2\) 以及 \(\urcorner \Phi_1\) 都是公式

• 域关系演算：以元组各分量为变量

  • 域演算表达式：\(\{(x_1, \dots x_k) \text{ | }\Phi(x_1, \dots x_k)\}\)

  • 原子公式：主要分为以下三类：

    1. R(\(x_1, \dots x_k\))，表示 \((x_1, \dots x_k)\) 是关系R的一个元组
    2. \(x_i \theta y_j\)，表示域变量 \(x_i\) 和 \(y_j\) 之间满足比较关系\(\theta\)
    3. \(x_i \theta c\) 或 \(c \theta x_i\)，表示域变量 \(x_i\) 和 常量 c 之间满足比较关系\(\theta\)

    注意：域演算与元组关系演算具有相同的运算符、以及相同的公式递归定义

• 关系运算的安全约束：

  • 安全表达式：不产生无限关系的表达式，不安全的表达式如 \(\{t \text{ | } \urcorner R(t)\}\)
  • \(\text{dom}(\Phi)\)：有限符号集，包含谓词公式\(\Phi\)中的所有显式常量 + 所有关系中元组的所有分量值
    注意：公式 \(\Phi\) 运算得到的最终关系、中间关系的所有元组各分量都必须属于\(\text{dom} (\Phi)\)

• 三类关系运算的等价性：经过安全约束的关系演算和关系代数的表达能力是等价的，可以相互转换

  

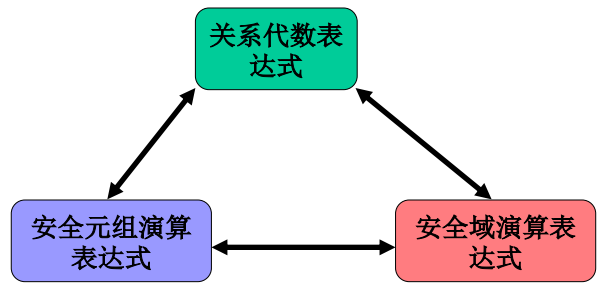
  三类关系运算

  注意：基本关系代数是过程化语言，元组关系演算和域关系演算是非过程化语言

---

五、关系数据语言

• 数据库数据语言：从功能上分为以下三种

  • 数据定义语言（DDL）：包括模式DDL、外模式DDL、内模式DDL
    注意：DDL用于定义数据库的三级模式，包括数据库的存储结构与访问方式
  • 数据操纵语言（DML）：支持数据库的检索、插入、删除、修改操作
    注意：DML语句被翻译为由低级指令构成的执行方案，由查询执行引擎执行
  • 数据控制语言（DCL）：完成数据库的安全性控制、完整性控制、并发控制等

• 关系数据语言的特点：

  • 一体化；将 Definition 和 Manipulation 融为一体，只给用户提供一种查询语言
  • 非过程化：只需用户指定需要什么数据，不用指明如何获得数据（声明式DML）
  • 面向集合的存取方式：操作对象是一个or多个关系、操作结果也是一个新的关系

• 查询语言：关系数据语言的核心是查询，关系运算是设计关系数据语言的基础

  关系运算的分类决定查询语言的分类