『compiler-2』lexer

词法分析

一、词法分析的功能

• 词法分析程序的功能：

  • 对词法进行分析：根据词法规则识别（组合）单词，并进行词法检查
  • 对常数值实现数字字符串到二进制数值的转变
  • 删除空格符 + 注释

• 单词：语言的基本语法单位，一般有四类单词：

  • 保留字：由源程序语言定义，如 BEGIN、IF 等
  • 标识符：由程序员定义的，表示各种名字的符号串
  • 常数：无符号数、布尔常数、字符串常数等
  • 分界符：如 + 、-、*、(、) 、< 等

• 单词的内部形式：单词类别 + 单词的值

  • 单词类别：按单词种类分类；保留字和分界符均采用一符一类
  • 单词值：标识符和常数自身的值（指针值）

---

二、文法与状态图

• 根据文法画出状态图：文法必须是左线性文法，即3型文法

  1. 设 G 的每一个非终结符都是一个状态
  2. 设一个开始状态 S
  3. 若 \(\text{Q} \rightarrow \text{t}\) ，其中 \(\text{Q} \in \text{V}_n\)、\(\text{t} \in \text{V}_t\)，则连接从 S 到 Q 的有向边，边上写 t
  4. 若 \(\text{Q} \rightarrow \text{Rt}\)，其中 \(\text{Q} \in \text{V}_n\)、\(\text{t} \in \text{V}_t\)，则连接从 R 到 Q 的有向边，边上写 t
  5. 连接好所有有向边之后，将开始符号对应的状态标记为终结状态

  注意：给定左（右）线性文法，可以将其改造为等价的右（左）线性文法

---

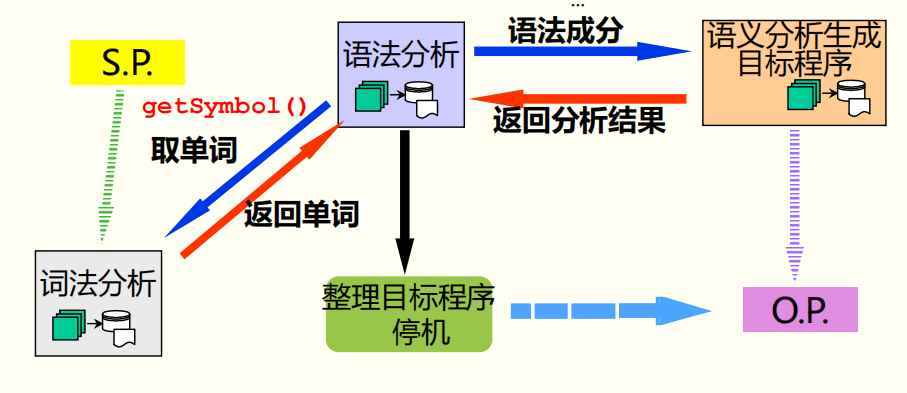
三、词法分析程序 getSymbol()

• 单遍扫描的词法分析程序：以词法分析为核心

  

• 词法规则：规定了四类单词的构造方式

• 词法状态图：根据词法规则构造
  注意：小的单词集合可被简单构造为无环转移图；无限的词类（如标识符、无符号整数）需要构造有环转移图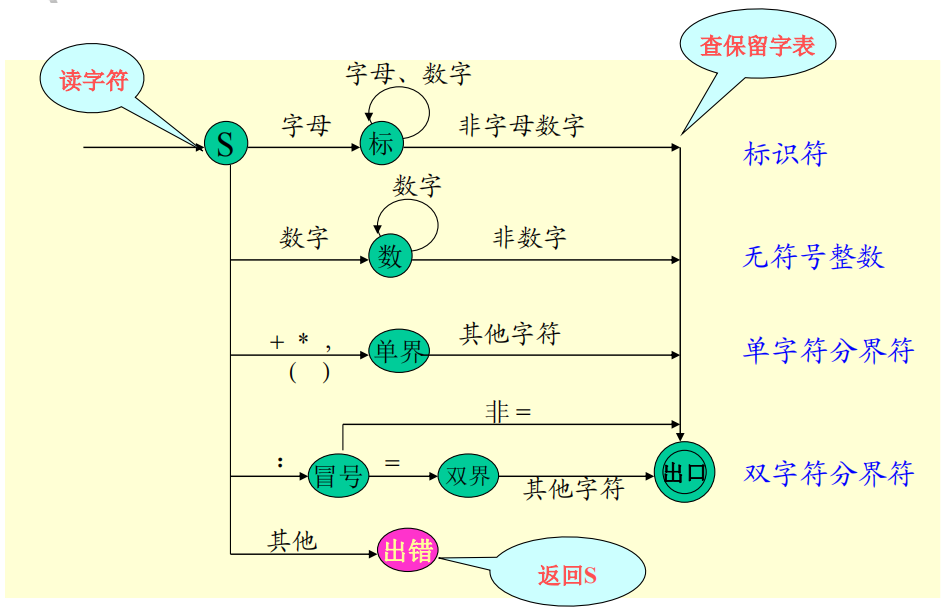

  

• 词法分析程序：设计单词分类、分析程序所需的全局变量、词法分析程序算法

---

四、有穷自动机

• DFA五元式：\(\text{M = } \{S, \Sigma, \delta, s_0, Z\}\)

  • S：表示确定自动机的有穷状态集合
  • \(\Sigma\)：表示输入字母表
  • \(\delta\)：映射函数，定义状态转移函数 \(\delta: S \times \Sigma \rightarrow S\) 若 \(\delta(s,a) = s'\)， 则 \(s, s' \in S\)，\(a \in \Sigma\)
  • \(s_0\)：初始状态，有 \(s_0 \in S\)
  • Z：终止状态集合，有 Z \(\subseteq S\)

  注意：对于确定的状态机，其确定性在于 \(\delta\) 是单值函数，且不允许 \(\epsilon\) 转移

• DFA与符号串：令 \(\alpha = \alpha_1 \alpha_2 \dots \alpha_n\)，其中 \(\alpha \in \sum^*\)，反复将当前迭代状态和当前输入字符一起送入\(\delta\)
  若 \(\delta(\delta(\dots \delta(s_0, a_1), a_2), \dots, a_{n-1}), a_n) = s_n\)，且 \(s_n \in Z\)，则可以写成 \(\delta(s_0, \alpha) = s_n\)，即串\(\alpha\)被自动机所接受
  注意：若存在一条从初始状态到某终止状态的路径，且该路径上各符号可连接成串\(\alpha\)，则称串\(\alpha\)可被自动机接受

• DFA接受的语言：L(M) = \(\{\alpha | \delta(s_0, \alpha) = s_n, s_n \in Z\}\)
  注意：由于DFA的 \(\delta\) 是一个单值函数，因此DFA在同一时刻只能有一个激活状态

  ---

• NFA五元式：M = \(\{S, \Sigma \cup \{\epsilon\}, \delta, s_0, Z\}\)

  • S：表示非确定自动机的有穷状态集合
  • \(\Sigma \cup \{\epsilon\}\)：表示输入符号集合与空串\(\epsilon\)
  • \(\delta\)：映射函数，定义状态转移函数 \(\delta: S \times \Sigma \cup \{\epsilon\} \rightarrow 2^{S}\)，其中 \(2^S\) 是 S 的幂集
  • \(s_0\)：初始状态，有 \(s_0 \in S\)
  • Z：终止状态集合，有 Z \(\subseteq S\)

  注意：对于不确定的状态机，其不确定性在于\(\delta\)是一个多值函数（状态对同一输入符号可能有多个后继状态），且允许特殊输入为 \(\epsilon\)（可以在无任何输入字符的情况下直接转移）

  

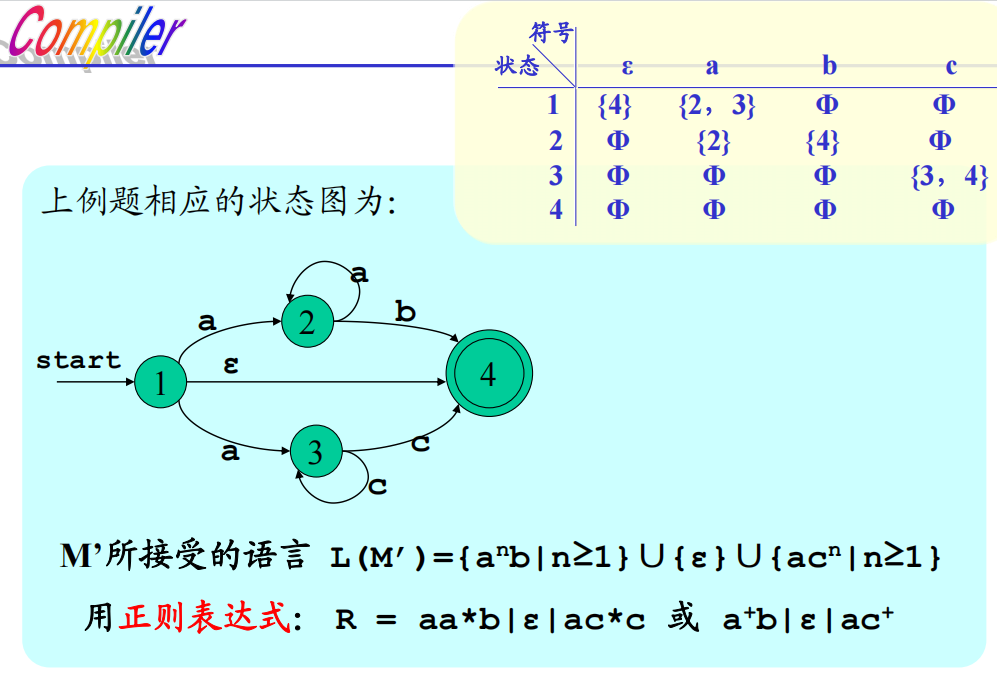
  NFA的状态转移

• NFA接受的语言：L(M') = \(\{\alpha | \delta(s_0, \alpha) = S', S' \cap Z \ne \varnothing\}\)
  注意：相较于DFA，NFA的同一时刻可以有多个激活状态，这些激活状态共同组成了集合\(S'\)

---

五、正则表达式

• 正则表达式的递归定义：设字母表为 \(\Sigma\)，有定义在 \(\Sigma\) 上的正则表达式和正则语言如下

  1. \(\epsilon\) 和 \(\varnothing\) 都是 \(\Sigma\) 上的正则表达式，其表示的正则语言分别为 \(\{\epsilon\}\) 和 \(\{\}\)（归纳基础）
  2. 对任意的 a \(\in \Sigma\)，a是 \(\Sigma\) 上的正则表达式，其表示的正则语言为 \(\{a\}\)
  3. 设 U 和 V均为 \(\Sigma\) 上的正则表达式，其表示的正则语言分别为 L(U) 和 L(V)
     则 U | V，UV 和 U* 均为 \(\Sigma\) 上的正则表达式，其对应的正则语言分别为 L(U) \(\cup\) L(V)，L(U) L(V) 和 L(U)*
  4. 任何 \(\Sigma\) 上的正则表达式与正则语言均由前三个步骤产生

  注意：正则表达式相同 \(\Leftrightarrow\) 两个正则表达式代表的正则语言相同

• 正则表达式和语言：设\(e_1\)和\(e_2\)为任意正则表达式，其产生的语言分别为\(L_1\)和\(L_2\)：

  1. \(e_1e_2 = \{xy \text{ | } x \in L_1 \land y \in L_2\}\)

  2. \(e_1 \text{ | } e_2 = \{x \text{ | }x \in L_1 \lor x \in L_2\}\)

  3. \(e_1^* = \{x \text{ | } x \in L_1^* \text{, }L_1^* = \bigcup_{i=0}^\infty L_1^i\}\)

• 正则表达式的运算符：重复 {n} 或 * \(\gt\) 连接 \(\cdot\) \(\gt\) 选择 | ，以及括号 ( )
  注意：正则运算符中的重复符号也可以用星号 * 表示，表示任意个符号连接的串

• 正则表达式的性质：设 \(e_1\)、\(e_2\)、\(e_3\) 均为字母表上的正则表达式

  • 单位正则表达式：即空串 \(\epsilon\)，且有 \(\epsilon e = e\epsilon = e\)
  • 选择交换律：\(e_1 | e_2 = e_2 | e_1\)
  • 结合律：对选择运算和连接运算分别有:
    1. 选择运算：\(e_1 | (e_2 | e_3) = (e_1|e_2) | e_3\)
    2. \(e_1(e_2e_3) = (e_1e_2)e_3\)
  • 分配律：只有连接对选择的分配律
    1. \(e_1(e_2|e_3) = e_1e_2|e_1e_3\)
    2. \((e_1|e_2)e_3 = e_1e_3 | e_2e_3\)
  • 其它：r* = (r | \(\epsilon\))*（星号表示可以为空串），r** = r*（重复幂等律），(r | s)* = (r*s*)*

• 根据正则表达式构造NFA：设 \(R_1\) 和 \(R_2\) 均为字母表\(\Sigma\)上的正则表达式，根据模板构造NFA

  • 基本规则：对于正则表达式的两条归纳基础：

    

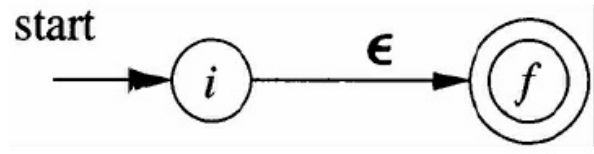
    空串规则

    

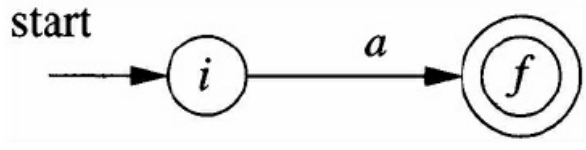
    字符规则

    • 归纳规则：对于正则表达式的三种归纳步骤：

      

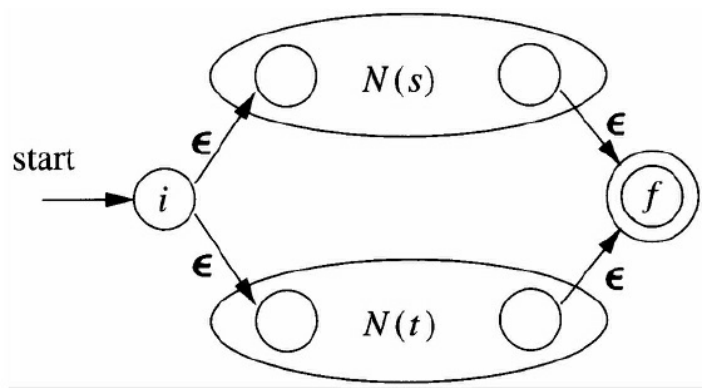
      并归纳

      合并后，原先的两个有穷自动机共享一个初始状态和接受状态

      ---

      

      连接归纳

​ 合并后，\(R_1\) 的结束状态和 \(R_2\) 的初始状态合并成一个中间状态

闭包归纳

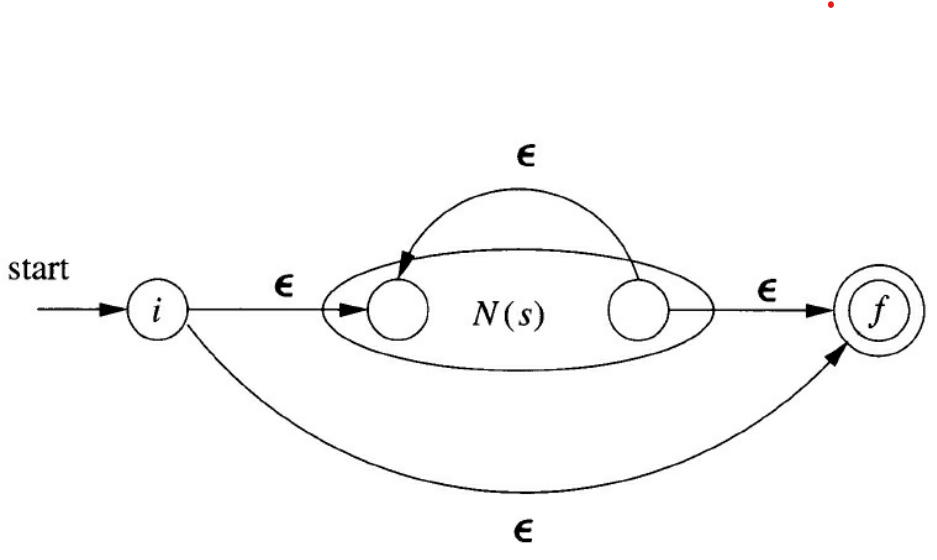
​ 可以直接绕过 \(R_1\) 到达接收状态，也可以循环经过 \(R_1\) 任意次再到达接收状态

---

六、NFA的确定化

• 状态集的 \(\epsilon\)-closure：\(\epsilon-\)closure(I)表示从状态合I中的状态出发，经过任意次 \(\epsilon\) 边所能到达的状态集合

• \(I_a\) 的定义：\(I_a = \epsilon-\)closure(J)，其中 J = \(\bigcup_{s \in I} \delta(s, a)\)，即从状态集I中的所有状态经过一次a转换得到的状态集合

• NFA转化为DFA：设NFA初始状态为\(s_0\)，DFA的初始状态\(I_0\)为 \(\epsilon-\)closure({\(s_0\)})，将\(I_0\)压入队尾：

  1. 将队首\(I\)移入DFA状态集合中，再将各 \(I_a = \epsilon-\)closure(\(\bigcup_{s \in I}\delta(s, a)\)) 压入队尾，其中 a 为输入字符
     注意：这一步只将尚不处在DFA状态集合的 \(I_a\) 压入队尾，避免重复入队
  2. 循环执行上一步操作，直至没有新的状态加入到队列中
     注意：扩展新状态是一个不动点计算的例子：到达某一时刻后后续迭代只能获得已经算出的状态
  3. 将DFA中包含原NFA中终止状态的状态全部标记为终止状态
  4. 对DFA的各状态重新标记（DFA的每个状态都是原NFA状态的集合）；确定新的转移函数

  

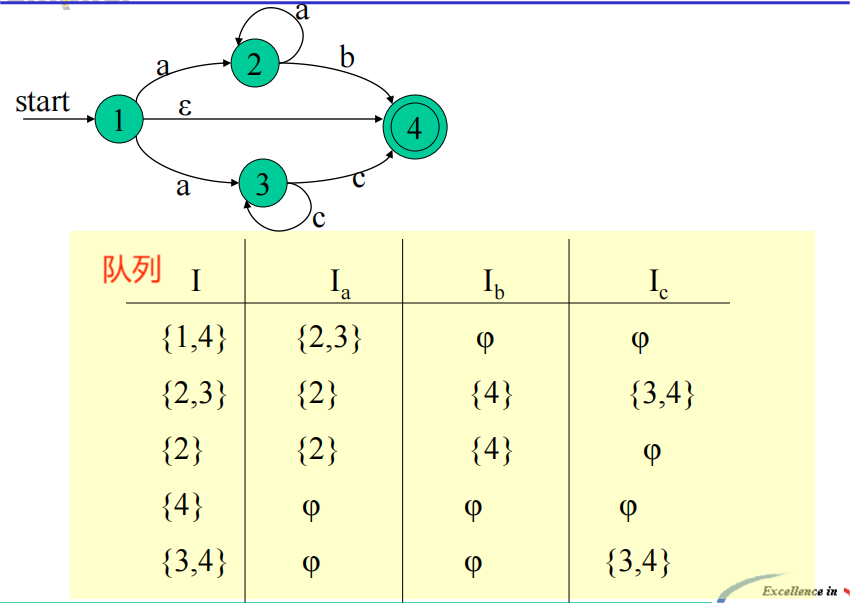
  DFA的每一个状态都是NFA状态集合的子集

  注意：DFA的状态数量最高可膨胀到\(2^{|{N}|}\)，其中\(|{N}|\)表示原NFA的状态数量

---

七、DFA的最小化

• 对于任何一个DFA，存在一个唯一的、状态最少的等价的DFA

• DFA的极小化：消除多余状态 + 合并等价状态

  • 多余状态：从DFA的开始状态出发，经过任何输入串也达不到的状态
  • 等价状态：状态s和t等价的充要条件，需同时满足一致性条件 + 蔓延性条件
    1. 一致性条件：s和t同时为接收状态 or 不接受状态
    2. 蔓延性条件：对于任意的输入符号，s和t必须转换到等价的状态中

• 分割法求解极小化DFA：通过划分DFA状态集合 \((s_0, ..., s_N)\) 求解

  1. 初始化：将DFA中的接收状态和非接受状态分别划入两个区（一致性）
  2. 反复划分：设已将DFA的各状态划入若干个互不等价的分区，每划分一次都重新检查各个分区：
  3. 若存在某个分区，其中有两个状态在同一输入下转移到不同的分区，则将该分区一分为二（蔓延性）
  4. 反复执行以上第 b c 步直至分区数量不再增加 注意：迭代分区也是一个不动点计算的例子：到达某一时刻后无法继续拆分分区
  5. 将包含原DFA接收状态的分区全部标记为接收状态；将包含原DFA初始状态的分区标记为初始状态
  6. 对化简后的DFA各分区重新标记（每个分区都是原DFA的状态集合）；确定新的转移函数

  

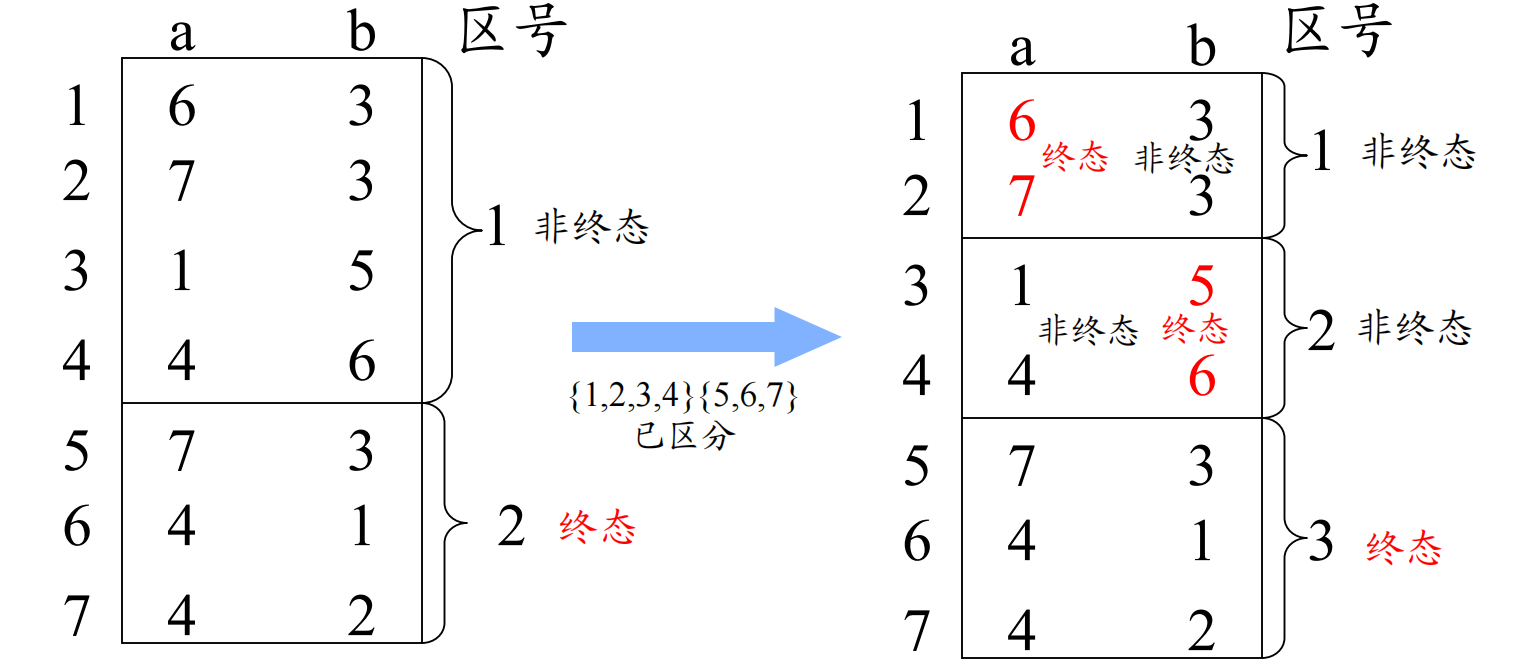
  总是将DFA的分区一分为二

  观察分区前的图片，获得分区的规律：对于任意分区，考察所有的输入符号

  • 无论输入字符是a还是b，状态1和2均转入了当前相同的分区，说明1和2当前不可再分；状态3和4同理
  • 对于输入字符a，状态1和2均转至分区2，而状态3和4均转至分区1，说明两者可被输入a分割（蔓延性）

---

八、词法分析程序的最小化

• LEX源程序：主要包含辅助定义式、识别规则、用户子程序
  • 辅助定义式：利用正则表达式描述各词类
  • 识别规则：根据识别到的单词，做出相应的行为（如 return Token）
• 词法分析自动生成器（LEX）：将LEX源程序转化为词法分析程序
  • 扫描每一条识别规则，分别构造对应的NFA
  • 将各NFA合并为一个完整的NFA
  • 将NFA转化为DFA
  • 生成DFA对应的状态转移矩阵和控制执行程序