『machine learning-2』model selection and evaluation
模型评估与选择
一、误差
误差:学习器实际预测输出与样本真实输出之间的差异
训练误差(经验误差):学习器在训练集上的误差
测试误差(泛化误差):学习器在测试集或新样本上的误差
注意:由于新样本是未知的,故常用 min(测试误差) 代替 min(泛化误差)
二、模型选择
对于同一个问题,可以选择多种算法
对于同一个算法,选择不同的参数配置
注意:对于机器学习问题,本质都是寻找一个映射 \(f: X \rightarrow Y\)
三、数据集划分
目标:将数据集 D 划分为训练集 S和测试集 T两部分
原则:测试集与训练集应尽量互斥,测试样本尽量不在训练集中出现
留出法:将 D 随机划分为训练集(\(\dfrac{2}{3}\))和测试集(\(\dfrac{1}{3}\));使用训练集导出模型,用测试集估计泛化误差
随机子抽样:将留出法重复进行k次,总准确率取各次准确率的平均值
k折交叉验证:将 D 划分为 k 个大小相似、互不相交的子集(“折”)
第 i 次迭代时,取第 i 折作为测试集,其余子集作为训练集;取 k 次测试的平均值留一法:k折交叉验证中,令 |D| = k,将 D 均分为 k 折,每一折仅有一个样本
自助法:从 D 中有放回地均匀抽样;采样 |D| 次后可获得大小为 |D| 的训练样本集
没有进入训练集的样本形成测试集- 优点:可产生多个不同的训练样本集;对于小数据集自助法效果胜过交叉验证
- 缺点:改变了数据集分布(随机抽样),会引入估计偏差
四、性能度量
回归任务:采用均方误差 \(E(f:D) = \dfrac{1}{d} \sum_{i=1}^{d}(f(x_i - y_i))^2\)
分类任务:采用错误率 \(E(f:D) = \dfrac{1}{d}\sum_{i=1}^{d} (f(x_i) \ne y_i)\)
其中 \(f\) 是训练的学习器、\(D\) 为初始样本集、\(y_i\) 表示样本输入 \(x_i\) 的真实标记注意:错误率和精度仅能评估是否正确分类,不能提供更精细的评估(如查全率、查准率等)
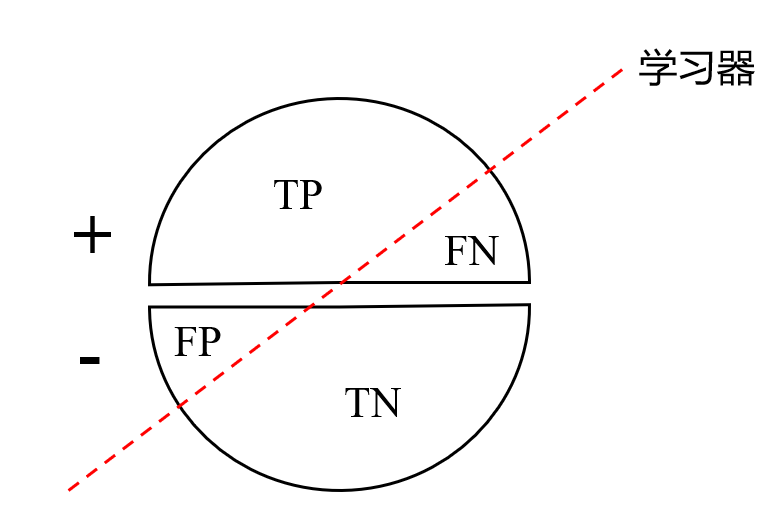
混淆矩阵:设仅有正负样本两类,分类表示方法为 <预测正误> + <预测结果>
- 真正例TP:被正确分类的正例
- 假负例FN:被错误标记为负例的正例
- 假正例FP:被错误标记为正例的负例
- 真负例TN:被正确分类的负例
敏感性(查全率):评估分类器正确识别正例的能力(即将尽可能多的正例挑选出来),避免漏识别 \[ \text{recall} = \frac{\text{TP}}{\text{P}} \]
特异性:评估分类器正确识别负例的能力(即将尽可能多的负例挑选出来) \[ \text{SP} = \frac{\text{TN}}{\text{N}} \]
准确率:评估分类器正确识别正负样本的能力(即正确 / 全体) \[ \text{accuracy} = \frac{\text{TP + TN}}{\text{P + N}} \]
精度(查准率):评估挑选出的正例中有多少是真正的正例,避免误识别 \[ \text{presicion} = \frac{\text{TP}}{\text{TP + FP}} \] 注意:查全率和查准率相互矛盾,此消彼长
要想查全率提高,只要将尽可能多的样本判断为正例,此时查准率下降
要想查准率提高,只能将最有把握的样本判断为正例,此时查全率下降P-R曲线:以召回率R为横轴、准确率P为纵轴的曲线图;曲线下方面积大、平衡点越大的模型效果越好
\(\text{F}_1\)度量:精确率与召回率的调和值,推荐系统中常用 \[ \text{F}_1 = \frac{2 \times \text{precision} \times \text{recall}}{\text{precision} + \text{recall}} \] \(\text{F}_\beta\) 度量:\(\text{F}_1\)度量的一般化形式,利用参数 \(\beta\) 控制查全率对查准率的相对重要性,\(\beta \gt 1\)说明查全率更重要 \[ \text{F}_{\beta} = \frac{(1 + \beta^2) \times \text{precision} \times \text{recall}}{\beta^2 \times \text{precision} + \text{recall}} \]
代价敏感性度量:引入预测错误的代价风险,\(\text{cost}_\text{FN}\) 表示将正例预测为负例的代价,\(\text{cost}_\text{FP}\) 则相反 \[ E(f:D) = \frac{1}{d} (\sum_{x_i \in D^+}(f(x_i) \ne y_i)\times \text{cost}_\text{FN} + \sum_{x_i \in D^-}(f(x_i) \ne y_i) \times \text{cost}_\text{FP}) \]
ROC曲线:TPR-FPR曲线
绘制流程:初始状态 = (0, 0),根据预测结果从大到小排序,将各分类阈值依次设在每个样例上,即依次将每个样例划分为正例
- 若当前样例是TP,对应标记点是\((\text{x}, \text{y} + \dfrac{1}{\text{m}^+})\),即向上平移,其中\(\text{m}^+\)表示正例数量
- 若当前样例是FP,对应标记点是\((\text{x}+\dfrac{1}{\text{m}^-}, \text{y})\),即向右平移,其中\(\text{m}^-\)表示负例数量
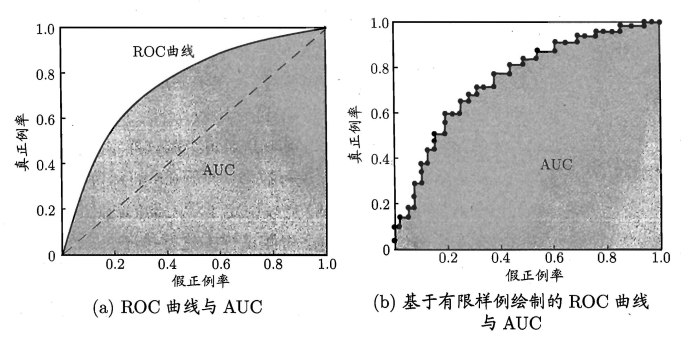
AUC:ROC曲线下方的面积,越大越好